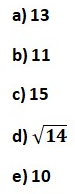28 de out. de 2021
28 de set. de 2021
SEQUÊNCIA NUMÉRICA
LEI DE FORMAÇÃO
Existem diversas sequências na natureza, mas as que nos interessam são
apenas as numéricas.
As sequências podem ser:
Finitas: ( 2, 4, 6, 8, 10) números pares menores que
12.
Infinitas: ( 1, 3, 5, 7, ... )
Usamos uma letra para índice numérico para localizar
um elemento da sequência.
Dada a sequência (a1,
a2, a3, a4, . . ., an, . . . )
Onde a1 é o primeiro termo
Onde a2 é o segundo termo
.
.
.
Onde an é o enésimo termo
Exemplo:
A sequência ( 0, 2, 4, ... ) pode ser obtida através da
expressão: an= 2n – 2
Para n =1
a1= 2.1 – 2 = 0
Para n =2
a2= 2.2 – 2 = 2
Para n =3
a3= 2.3 – 2 = 4
Para n =4
a4= 2.4 – 2 = 6
Para n =5
a5= 2.5 – 2 = 8 e assim por
diante.
1) Determine
a lei de formação das sequências abaixo:
a) (6, 12, 18,
24, 30, 36, . . .)
Resp.: an = 6n
b) (7, 8,
9, 10,11, 12, . . .)
Resp.: na
= 6 + n
d)(4, 8, 12, 16, . . .
)
Res.: an
= 4n
2) Escreva
os cincos primeiros termos das sequências dadas pelas leis de formação:
a) an= 3n – 2
a1
= 3. 1 – 2 = 1
a2 =
3.2 – 2 = 4
a3 =
3.3 – 2 = 7
a4 =
3.4 – 2 = 10
a5 =
3.5 – 2 = 13
S : ( 1, 4, 7, 10, 13 )
b) an= 2n + 3
an= 2n + 3
a1 = 2.1 + 3 = 5
a2 = 2.2 + 3 = 7
a3 = 2.3 + 3 = 9
a4 = 2.4 + 3 = 11
a5 = 2.5 + 3 = 13
S: ( 5, 7, 9, 11, 13 )
c) an
= 2n + 1
a1
= 2.1 + 1 = 3
a2
= 2.2 + 1 = 5
a3
= 2.3 + 1 = 7
a4
= 2.4 + 1 = 9
a5
= 2.5 + 1 = 11
S: ( 3, 5,
7, 9, 11 )
d) n2
n2 = 12
= 1
n2 = 22
= 4
n2 = 32
= 9
n2 = 42
= 16
n2 = 52
= 25
S : ( 1, 4, 9, 16, 25 )
( pequeno resumo de sequência numérica para o 7° ano)
31 de ago. de 2021
LÓGICA QUANTITATIVA
1) Observe o desenho da balança abaixo, sabendo-se que ela está em equilíbrio.
Sabendo-se que cada bolinha é igual dois quadradinho. Esta balança esta marcando quantas unidades de massa?
a) 12 unidades de massa;
b) 15 unidades de massa;
c) 18 unidades de massa;
d) 21 unidades de massa;
2) A balança abaixo está em equilíbrio. As bolas tem o mesmo peso. Os sacos têm a mesma quantidades de bolas iguais as de fora, os sacos vazios têm peso desprezível.
Quantas bolas cada saquinho contém?
a) 5.
b) 4.
c) 3.
d) 2.
Ver as aqui Respostas
1) Letra D
2) Letra B
12 de ago. de 2021
CUBO: EXERCÍCIOS
1) Sabendo que um cubo tem 2 cm de aresta. Então quanto mede:
a) Área total
b) Volume
c) A diagonal
2) O volume de um cubo mede 27 cm3 . Então quanto mede:
a) A aresta
b) Área total
c) A diagonal
3) (PUC -SP) Um cubo tem área total igual a 72 m2 . Sua diagonal vale:
4) Qual o volume de um cubo sabendo que sua área total mede 54cm2?
5) Calcule a área de um cubo, sabendo-se que uma diagonal de mede 9cm?
RESPOSTAS:
1) Sabendo que um cubo tem 2 cm de aresta. Então quanto mede:
a) Área total
At = 6. a2
At = 6. 22
At = 6. 4
At = 24 cm2
b) Volume
V = a3
V = 23
V = 8 cm3
c) A diagonal
2) O volume de um cubo mede 27 cm3 . Então quanto mede:
a) A aresta
b) Área total
At = 6.a2
At = 6.32
At = 6.9
At
= 54 cm2
c) A diagonal
3) (PUC -SP) Um cubo tem área total igual a 72 m2 . Sua diagonal vale:
Antes preciso achar o valor da aresta.
Resposta correta letra B.
4) Qual o volume de um cubo sabendo que sua área total mede 54cm2?
Preciso encontrar a aresta.
5) Calcule a área de um cubo, sabendo-se que uma diagonal de mede 9cm?
10 de jul. de 2021
CUBO
O cubo é um prisma com os seis lados congruentes, logo se trata de um prisma regular.
Fórmulas para calcular a área total, o volume e a diagonal de um cubo.
Área total é seis vezes a área de um dos quadrados do cubo.
Volume de um cubo é dado pelo produto (multiplicação) da altura ( aresta) pela área da base.
A Diagonal de um cubo é calculada usando a seguinte fórmula;
Exemplos:
1) Calcule a área total e o volume de um cubo sabendo que sua aresta mede 5cm.
2) (Vunesp-SP) Quantos cubos A precisa-se empilhar para formar o paralelepípedo B?
a) 60 b) 47 c) 94 d) 39 e) 48
Para encontrar o número total de cubos A que formar o paralelepípedo basta multiplicar os lados.
T= 5 x 3 x 4
T = 60
Será preciso de 60 cubos A para formar o paralelepípedo.
Resposta certa letra A.
21 de mai. de 2021
14 de mai. de 2021
12 de mai. de 2021
DIAGONAL DO PARALELEPÍPEDO RETÂNGULO
Usando o teorema de Pitágoras, o triângulo ABC é retângulo, sendo assim, a medida da diagonal é representado pela fórmula:
Exemplo:
a) qual é a diagonal de um paralelepípedo retângulo que apresenta aresta lateral 3cm e arestas de base 2 cm e 5 cm?
1- Dado um paralelepípedo retângulo de dimensões 4 m, 6 m e 12 m, calcule.
a) volume
b) área total
c) a diagonal
Solução:
a) volume
b) área total
c) a diagonal
2) (UFV-MG) Se no paralelepípedo retângula a = 1, b = 2 e c = 3, o comprimento do segmento AC é:
23 de abr. de 2021
17 de abr. de 2021
UM POUCO DE SEMELHANÇA DE TRIÂNGULOS
Na atividade abaixo vamos ver um pouco de semelhança dos triângulos:
1) Dados os quadrados da figura, calcular o valor de x.
Respostas
1)Dados os quadrados da figura, calcular o valor de x.
Os triângulos 1 e 2 são semelhantes
2) As bases de um trapézio medem 12m e 18m e os lados oblíquos às bases medem 5m e 7m. Determine os lados do menor triângulo que obtemos ao prolongar os lados oblíquos às bases.
Os lados EF // AC são paralelos
Os triângulos ADC ~ EDF são semelhantes
12 de mar. de 2021
DESCOBRINDO O RESTO DA DIVISÃO DE UM NÚMERO
II- Parte
O resto da divisão de um número é sempre uma unidade menor que o divisor.
V) Divisão por 8, para isso divide-se os três últimos números da direita, para encontrar o resto da divisão.
a) Qual o resto da divisão de 29.258 por 8?
Dividindo os três últimos número da direita vamos encontrar:
Logo, o resto é 2.
b) Qual o resto da divisão de 8.594 por 8?
O quociente é 1.074 o resto é 2.
VI) Divisão por 9. Se for maior ou igual a 9 ou se for menor que 9.
*Quando for maior ou igual a 9.
* Soma-se os números, e a soma dos valores absolutos é divide-se por 9, e o resto será dado pelo resto da divisão dessa soma por 9.
a) Qual o resto da divisão de 29.255 por 9?
Valor absoluto: 2+9+2+5+5 = 23
Logo, o resto é 5.
b) Qual o resto da divisão de 3.078 por 9?
Valor absoluto: 3+0+7+8 = 18 = 1+8 = 9
*Quando for menor que 9.
* Quando a soma do valor absoluto for menor que 9, o resto será a soma desses números.
a) Qual o resto da divisão de 21.014 por 9?
Valor absoluto: 2+1+0+1+4 = 8
b) Qual o resto da divisão de 5.0020 por 9?
Valor absoluto: 5+0+0+2+0 = 7
Logo, o resto da divisão é 7.
VII) Resto da divisão de um número por 10.
O resto é o número da unidade.
a) Qual é o resto de 63.207 por 10?
Veja que o número 63.207 terminou em 7, logo, o resto dessa divisão é 7.
b) Qual é o resto de 31.985 por 10?
Como o número 31.985 termina em 5, o resto é 5.
VIII) Resto da divisão por 11.
a) Qual o resto da divisão de 87.423 por 11?
Ordene os números de trás para frente conforme o exemplo:
Subtraindo:
ímpar - par
15 - 9 = 6
Logo, o resto da divisão é 6.
3 0 2 9
ímpar: 0 + 9 = 9
par: 2+3 = 5
9 - 5 = 4
Logo, o resto da divisão é 4.
24 de fev. de 2021
DESCOBRINDO O RESTO DA DIVISÃO DE UM NÚMERO
I- Parte
O resto da divisão de um número é sempre uma unidade menor que o divisor.
I) Divisão por 2, quando o último algarismo da direita for par, o resto será zero; quando for ímpar, o resto será um.
Vamos calcular o resto da divisão por 2 dos números:
a) 3428
b) 7653
Resposta:
a) 3428 a divisão por 2 o resto é zero, pois é um número par.
b) 7653 a divisão por 2 o resto é 1, pois é um número ímpar.
II) Divisão por 3, soma-se os algarismos e divide a soma por 3.
a) 6591
b) 8597
Resposta:
a) 6591 somando os algarismos: 6+5+9+1 = 21
Dividindo 21 por 3 o quociente é 7 e o resto zero
b) 8597 somando os algarismos 8+5+9+7 = 29
Dividindo 29 por 3 o quociente é 9 e o resto é 2.
III) Divisão por 4, basta dividi os dois últimos números formado pelos algarismos da direita.
a) 876549
b) 628535
Resposta:
a) 876549 dividindo 49 por 4 o quociente é 12 e o resto 1.
b) 628535 dividindo 35 por 4 o quociente é 8 e o resto 3.
IV) Divisão por 5, para esse caso existe algumas possibilidades.
*Se o último algarismo da direita for maior que 5, subtrai esse número do 5.
a) 65439 subtraindo 9 - 5 = 4 o resto é 4.
*Se o último algarismos for menor que 5. Podemos dividi os dois últimos algarismos da direita por 5.
b) 65432 dividindo 32 por 5 o quociente é 6 e o resto é 2.
*Podemos pegar também os dois últimos algarismos da direita e dividi por 5.
c) 98759 dividindo 59 por 5, o quociente é 11 e o resto 4.
9 de fev. de 2021
EXERCÍCIOS DE DIVISIBILIDADE
1) Determine o algarismo de x de modo que o inteiro 8x6 seja divisível por 3 e 4, simultaneamente.
2) Determine os menores valores para x e y de modo que o inteiro 231xy seja divisível por 5 e 9 ao mesmo tempo.
3) Sendo o número 4a8b divisível simultaneamente por 2, 3, 5, 9 e 10. Calcule a e b.
4) Determine os algarismos que devem ser escritos no lugar de x e y, no número x64y, que é menor do que 4.000, para que seja, ao mesmo tempo, divisível por 5 e 9.
5) Verifique se 4968, 2472 e 6172 são divisível por 12.
SOLUÇÃO:
1) Determine o algarismo de x de modo que o inteiro 8 x 6 seja divisível por 3 e 4, simultaneamente.
Para um número ser divisível por 3 a soma dos valores absoluto deve ser um número divisível por 3.
8 0 6 (8 + 0 + 6 = 14 ), ( o 0 não serve)
8 1 6 (8 + 1 + 6 = 15), ( o 1 serve ), os dois últimos números da direta é divisível por 4.
8 2 6 ( 8 + 2 + 6 = 16), ( o 2 não serve )
8 3 6 ( 8 + 3 + 6 = 17 ), ( o 3 não serve )
8 4 6 ( 8 + 4 + 6 = 18), ( o 4 não serve )
8 5 6 ( 8 + 5 + 6 = 19), ( o 5 não serve )
8 6 6 ( 8 + 6 + 6 = 20), ( o 6 não serve )
8 7 6 ( 8 + 7 + 6 = 21), ( o 7 serve ) os dois últimos números da direta é divisível por 4.
8 8 6 ( 8 + 8 + 6 = 22 ), ( o 8 não serve )
8 9 6 ( 8 + 9 + 6 = 23), ( o 9 não serve )
x =1
x= 7
2) Determine os menores valores para x e y de modo que o inteiro 231xy seja divisível por 5 e 9 ao mesmo tempo.
Para um número ser divisível por 9 a soma dos valores absoluto deve ser um número divisível por 9.
Para a divisão por 5 o número tem que ter final 0 ou 5.
231xy
23130 ( 2+3+1+3+0= 9) , também é divisível por 5.
23175 (2+3+1+7+5 = 18), também é divisível por 5.
x=3 y=0
3) Sendo o número 4a8b divisível simultaneamente por 2, 3, 5, 9 e 10. Calcule a e b.
Para b só pode ser 0.
Logo, vai ser por 2 e por 5.
4a8b
4680 ( 4+6+8+0=18), pode ser divisível por 3 e por 9
a=6 b= 0
4) Determine os algarismos que devem ser escritos no lugar de x e y, no número x64y, que é menor do que 4.000, para que seja, ao mesmo tempo, divisível por 5 e 9.
Para ser divisível por 5 o y de ser igual a 5 ou a 0
x64y
3640 ( 3+6+4+0 = 13), é divisível por 5, mas não é por 3.
3645 ( 3+6+4+5 = 18), é divisível por 3 e por 5
x=3 y=5
5) Verifique se 4968, 2472 e 6172 são divisível por 12.
Um número é divisível por 12 quando for divisível por 3 e por 4 ao mesmo tempo.
4968 ( 4+9+6+8 = 27), é divisível por 3 e como 68 também é divisível por 4, logo é por 12.
2472 ( 2+4+7+2 = 15), é divisível por 3 e como 72 também é divisível por 4, logo é por 12.
6172 ( 6+1+7+2= 16), 72 é divisível por 4, mas a soma dos valor absoluto não é divisível por 3.
12 de jan. de 2021
EXERCÍCIOS COM POTENCIAÇÃO
Usando os conhecimentos das regras de potência:
1) A metade de 222 é:
a) 1
b) 11
c) 221
d) 211
2) A metade de 1620 é:
a) 810
b) 279
c) 164
d) 820
3) Simplificando
, obtemos:
, obtemos:a) 236
b) 224
c) 168
d) 86
Resolução:
1) A metade de 222 é
Significa que vamos dividir o número por 2.
2) A metade de 1620 é:
Vamos dividir por 2. Mas antes vamos fatorar 16 para igualar as bases.
Resposta: B
3) Simplificando, obtemos:
, obtemos:3 elevado ao quadrado é 9
(24)9
Potência de uma potência é só multiplicar os expoentes.
236
Resposta: A
Potência de uma potência
3 -4
Para eliminar o sinal negativo do expoente escrevemos em forma de uma fração, lembrado que tanto o numerador quanto o denominador é elevado a 4.
Resposta: B