1) O quadrado e o retângulo abaixo têm a mesma área. Sendo assim calcule a medida do lado do quadrado e sua área.
2) (Funrio/Auxiliar/2008) A área do terreno, cuja planta é apresentado na figura abaixo, em m2 vale:
3) A tela de um
quadro tem a forma
retangular e mede 50 cm e 30. Nela foi colocado uma
moldura, também retangular, de largura x. Calcule essa largura, sabendo que o quadro todo passou a ocupar uma área de 2400
cm2.
1) O quadrado e o retângulo abaixo têm a mesma área. Sendo assim calcule a medida do lado do quadrado e sua área.
A área do quadrado é x2
A área do retângulo 16 ( x + 5 ) = 16x + 80
A questão fala que a área do quadrado é igual a do retângulo, sendo assim vamos igualar para encontra o valor de x.
x2= 16x + 80 agora temos uma equação do 2º grau.
x2 - 16x - 80 = 0 usando a fórmula de Bhaskara.
O lado do quadrado mede 20Para encontra a área do quadrado é só multiplicar um lado elo outro.
x . x = x2
20 . 20 = 400
Como a questão diz que o retângulo tem a mesma medida, logo a área do retângulo é também 400.
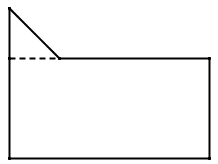
Podemos separa a figura em duas.
Agora temos um retângulo e um triângulo.
Para achar a área do retângulo é só multiplicar a base pela altura.
3 . 2 = 6 cm2
Para encontrar a área do triângulo é só multiplicar a base pela altura e dividi por 2.
Agora é só somar a área do retângulo com a do triângulo
6 + 0,5 = 6,5 cm2
3) A tela de um quadro tem a forma retângula e mede 50 cm e 30. Nela foi colocado uma moldura, também retangular, de largura x. Calcule essa largura, sabendo que o quadro todo passou a ocupar uma área de 2400 cm2.
Lembrado a área é base pela altura.
(30 + 2x) (50 + 2x) = 2400
x representa a largura da moldura
x = 5 cm
