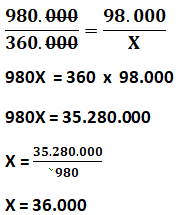A regra da sociedade, tem por objetivo a distribuição em partes proporcionais, dos lucros ou prejuízos de uma sociedade. A regra de sociedade é pode ser: Simples ou Composta:
A SIMPLES pode ser:
1º Capitais iguais e tempos iguais
2º Capitais iguais e temos diferentes
3º Capitais diferentes e tempos iguais
A COMPOSTA: Capitais diferentes e tempos diferentes.
1º Capitais iguais e tempos iguais
Exemplo: Cinco pessoas fundaram uma sociedade, cada um entrou com R$ 800,00. No final de sete meses tiveram um lucro de R$ 4.500,00. Quanto cada um receberá de lucro?
Solução:
Veja que tanto o capital e o tempo são os mesmos, basta dividir o lucro pelo total de sócios.
4.500, 00 : 5 = 900
Logo cada sócio ira receber R$ 900,00
2º Capitais iguais e temos diferentes
Exemplo: Três amigos entraram em uma sociedade cada um com o capital de R$ 1.500,00 mas tiveram um prejuízo de R$ 750,00. Sabendo que o primeiro ficou 8 meses na sociedade, o segundo 7 meses e, o terceiro, 9 meses. Determine o prejuízo de cada um.
Solução:
Como os três sócios entraram com o mesmo valor. Basta somar o tempo que cada um ficou na sociedade e o resultado multiplicar pelo tempo de cada um.
8 meses + 7 meses + 9 meses = 24
750,00 : 24 = 31,25
Primeiro: 8 meses
8 x 31,25 = 250
Segundo: 7 meses
7 x 31,25 = 218,75
Terceiro: 9 meses
9 x 31,25 = 281,25
Somando o resultado dos três a soma deve ser igual a 750
250 + 218,75 + 281,25 = 750
Logo;
O Primeiro: teve um prejuízo de R$ 250,00
O Segundo: teve um prejuízo de R$ 218,75
O Terceiro: teve um prejuízo de R$ 281,25
3º Capitais diferentes e tempos iguais
Duas pessoas se uniram e formaram uma sociedade e lucraram R$ 2.500,00 . A primeira pessoa entrou com R$ 700,00 e a segunda com R$ 550,00. Calcule o lucro de cada uma.
Solução:
Como a questão não cita o tempo, logo o tempo foi igual para ambos.
Montando a proporção e resolvendo para o primeiro sócio:
Dados:
700,00 + 550,00 = 1,250 capital inicial dos dois
2.500,00 lucro para ser dividido entre os dois
Montando a proporção e resolvendo para o segundo sócio:
O primeiro sócio recebeu R$ 1.400,00
O segundo sócio recebeu R$ 1.100,00
A COMPOSTA: Capitais diferentes e tempos diferentes.
Três negociantes fundaram uma sociedade. O primeiro entrou com um capital de R$ 30.000,00 permanecendo por 12 meses. O segundo com um capital de R$ 40.000,00, durante 8 meses e o terceiro com um capital de R$ 50.000,00 durante 6 meses. No final, a sociedade deu um lucro de R$ 98.000,00. Calcule quanto cada um recebeu de lucro.
Solução:
Multiplica o capital inicial de cada um pelo tempo e o resultado adiciona-se
Montando a proporção com os dados que temos:
Soma total R$ 980.000,00
Lucro R$ 98.000,00
Montando a proporção e resolvendo para o primeiro sócio:
Eliminamos os três zeros do numerador e do denominador para facilitar os cálculos.
Montando a proporção e resolvendo para o terceiro sócio:
O primeiro sócio recebeu: R$ 36.000,00
O segundo sócio recebeu R$ 32.000,00
O terceiro sócio recebeu R$ 30.000,00