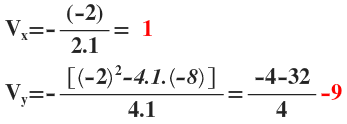A função
polinomial do 2º grau ou função quadrática é toda função escrita y=ax2 +
bx + c, ou
f(x) = ax2 + bx +
c
sendo a, b e c números reais.
São exemplos de funções do 2º grau:
a) y=x2 +
2x – 8
b) y= x2 – 9 c)
y=-3x2 -2x + 1
GRÁFICO DA FUNÇÃO QUADRÁTICA
O gráfico da
função do 2º grau é representado por uma curva chamado de parábola.
ZEROS DA FUNÇÃO POLINOMIAL DO 2º GRAU
Quando delta for maior que zero a função y= ax2 + bx + c, tem
duas raízes reais diferentes, isto é, o gráfico corta o eixo de x em dois
pontos.
Quando delta for menor que zero a função y= ax2 + bx + c, não tem raízes reais.
Quando delta for igual a zero a função y= ax2 + bx + c, tem
uma única raiz real diferente, o gráfico
tangencia o eixo de x.
Exemplo: Determinar as raízes da função a
seguir: y = x2 + 2x – 3
Igualando a função a zero, transformamos em uma equação de 2º grau
x2 + 2x – 3=0
Identificando os termos da função;
a=1 b=2 c=-3
Podemos usar a fórmula de Bhaskara para encontrar as raízes.
Igualando a função a zero, transformamos em uma equação de 2º grau
x2 + 2x – 3=0
Identificando os termos da função;
a=1 b=2 c=-3
Podemos usar a fórmula de Bhaskara para encontrar as raízes.
Obs: Nesta função o gráfico corta o eixo de
x( eixo das abscissas) em dois pontos
são -3 e 1. Veja o gráfico abaixo como ficou:
2. Determinar as raízes da função a
seguir:
Igualando a função a zero: x2 + 3x + 5=0
Termos: a=1 b=3 c= 5
A equação não tem solução no conjunto dos reais, sendo assim observe como fica o gráfico dessa função.
Obs: Nesta função o gráfico não corta o eixo
de x( eixo das abscissas. Veja o gráfico.
3.
Determinar as raízes da função a seguir:
Igualando a função a zero: x2 -4x + 4=0
Termos: a=1 b=-4 c= 4
Obs: Nesta função o gráfico corta o eixo de
x( eixo das abscissas) em um único ponto 2. Veja o gráfico.
O quadro
abaixo mostra todas as possibilidades considerando sua concavidade.
Obs: Quando a>0 significa que a parábola tem a concavidade voltada para cima.
Quando a < 0,
significa que a parábola tem a concavidade voltada para baixo.
COMO CONSTRUIR O GRÁFICO DA FUNÇÃO
1- Construir, no plano cartesiano, o
gráfico da função y =x2 - 9
Atribuindo alguns valores para x,
encontramos o valor de y.
y =x2 - 9
Y = (-4)2 – 9 = 16 – 9 = 7
Y
= (-3)2 – 9 = 9 – 9 = 0
Y = (-2)2 – 9 = 4 – 9 = -5
Y
= (0)2 – 9 = 0 – 9 = -9
Y = (2)2 – 9 = 4 – 9 = -5
Y
= (3)2 – 9 = 9 – 9 = 0
Y = (4)2 – 9 = 16 – 9 = 7
veja como fica a tabela abaixo. No plano cartesiano vamos marcar os pontos encontrados e traçar o gráfico.
x
|
y
|
(x,Y)
|
-4
|
7
|
(-4,7)
|
-3
|
0
|
(-3,0)
|
-2
|
-5
|
(-2, -5)
|
0
|
-9
|
(0, -9)
|
2
|
-5
|
(2,-5)
|
3
|
0
|
(3, 0)
|
4
|
7
|
(4,7)
|
Veja que o gráfico
corta o eixo das abscissas nos pontos -3 e 3, enquanto que o ponto mínimo da
parábola tangencia o eixo de y em -9.
2-
Construir o gráfico da função: y= x2 + 4x – 5
O gráfico
corta o eixo das abscissas nos pontos -5 e 1, enquanto que o ponto mínimo da
parábola tangencia o eixo de y em -9.
Quando
a parábola tem a concavidade voltada para cima dizemos que a função possui um
MÍNIMO.
3- Construir, no plano cartesiano, o
gráfico da função y =-x2 - 4
Atribuindo alguns valores para x,
encontramos o valor de y. Depois traçar o gráfico e marcar os pontos.
y =-x2 - 4
Y = -(4)2 – 4 = -16 – 4 =
-20
Y = -(3)2 – 4 = -9 – 4 = -13
Y = -(2)2 – 4 =- 4 – 4 =
-8
Y
= -(0)2 – 4 = 0 – 4 = -4
x
|
y
|
(x,Y)
|
-4
|
-20
|
(-4, -20)
|
-3
|
-13
|
(-3, -13)
|
-2
|
-8
|
(-2, -8)
|
0
|
-4
|
(0, -4)
|
4-
Construir o gráfico da função: y= - x2 + 4x – 5
O gráfico
tem como vértices (2, -1)
O gráfico
não corta o eixo das abscissas no ponto, isto é, não tem raízes nos reais.
Quando
a parábola tem a concavidade voltada para baixo dizemos que a função possui um
MÁXIMO.
1º Determinar as coordenadas do Vértice: V(Xv,
Yv).
2º Organizar uma tabela, onde se atribuir alguns
valores menores que Xv e
alguns valores maiores que Xv .
3º Marcar os pontos no plano cartesiano no eixo das x
(abscissas) e eixo das y( ordenadas).
4º para finalizar é só ligar os pontos construindo a
parábola.
O VÉRTICE
DA PARÁBOLA: As
coordenadas do vértice da parábola são dadas por:
Exemplos:
1) Achar o máximo ou o mínimo da função f(x)=x2 – 2x
– 8
A função tem o mínimo igual a -9.
Outra maneira para encontrar o vértice de y, substituir o valor encontrado de x na
função. Veja como fica:
f(x)=x2 – 2x – 8
y= 12 – 2 .1 – 8
y= 1 – 2 – 8 = -9
Vejamos o gráfico dessa função:
A função tem o mínimo igual a -9.
Outra maneira para encontrar o vértice de y, substituir o valor encontrado de x na
função. Veja como fica:
f(x)=x2 – 2x – 8
y= 12 – 2 .1 – 8
y= 1 – 2 – 8 = -9
2) Achar o máximo ou o mínimo da função f(x)= - x2
+ 6x – 9
A função tem o máximo igual a 3.
Outra maneira para encontrar o vértice de y, substituir o valor encontrado de x na
função. Veja como fica:
f(x)=-x2 – 6x – 9
y= 32 – 6 .(-3) – 9
y= - 9 +18 – 9 = 0
3)
Achar o máximo ou o mínimo da função f(x)= - x2 - 2x +1
A função tem o máximo
igual a 2.
4) Achar o máximo ou o mínimo da função f(x)= x2 + 3x - 4
Em uma outra postagem estudaremos OS SINAL DA FUNÇÃO.