A função
polinomial do 2º grau ou função quadrática é toda função escrita y=ax2 +
bx + c, ou
f(x) = ax2 + bx +
c
sendo a, b e c números reais.
São exemplos de funções do 2º grau:
a) y=x2 +
2x – 8
b) y= x2 – 9 c)
y=-3x2 -2x + 1
GRÁFICO DA FUNÇÃO QUADRÁTICA
O gráfico da
função do 2º grau é representado por uma curva chamado de parábola.
ZEROS DA FUNÇÃO POLINOMIAL DO 2º GRAU
Quando delta for maior que zero a função y= ax2 + bx + c, tem
duas raízes reais diferentes, isto é, o gráfico corta o eixo de x em dois
pontos.
Quando delta for menor que zero a função y= ax2 + bx + c, não tem raízes reais.
Quando delta for igual a zero a função y= ax2 + bx + c, tem
uma única raiz real diferente, o gráfico
tangencia o eixo de x.
Exemplo: Determinar as raízes da função a
seguir: y = x2 + 2x – 3
Igualando a função a zero, transformamos em uma equação de 2º grau
x2 + 2x – 3=0
Identificando os termos da função;
a=1 b=2 c=-3
Podemos usar a fórmula de Bhaskara para encontrar as raízes.
Igualando a função a zero, transformamos em uma equação de 2º grau
x2 + 2x – 3=0
Identificando os termos da função;
a=1 b=2 c=-3
Podemos usar a fórmula de Bhaskara para encontrar as raízes.
Obs: Nesta função o gráfico corta o eixo de
x( eixo das abscissas) em dois pontos
são -3 e 1. Veja o gráfico abaixo como ficou:
2. Determinar as raízes da função a
seguir:
Igualando a função a zero: x2 + 3x + 5=0
Termos: a=1 b=3 c= 5
A equação não tem solução no conjunto dos reais, sendo assim observe como fica o gráfico dessa função.
Obs: Nesta função o gráfico não corta o eixo
de x( eixo das abscissas. Veja o gráfico.
3.
Determinar as raízes da função a seguir:
Igualando a função a zero: x2 -4x + 4=0
Termos: a=1 b=-4 c= 4
Obs: Nesta função o gráfico corta o eixo de
x( eixo das abscissas) em um único ponto 2. Veja o gráfico.
O quadro
abaixo mostra todas as possibilidades considerando sua concavidade.
Obs: Quando a>0 significa que a parábola tem a concavidade voltada para cima.
Quando a < 0,
significa que a parábola tem a concavidade voltada para baixo.
COMO CONSTRUIR O GRÁFICO DA FUNÇÃO
1- Construir, no plano cartesiano, o
gráfico da função y =x2 - 9
Atribuindo alguns valores para x,
encontramos o valor de y.
y =x2 - 9
Y = (-4)2 – 9 = 16 – 9 = 7
Y
= (-3)2 – 9 = 9 – 9 = 0
Y = (-2)2 – 9 = 4 – 9 = -5
Y
= (0)2 – 9 = 0 – 9 = -9
Y = (2)2 – 9 = 4 – 9 = -5
Y
= (3)2 – 9 = 9 – 9 = 0
Y = (4)2 – 9 = 16 – 9 = 7
veja como fica a tabela abaixo. No plano cartesiano vamos marcar os pontos encontrados e traçar o gráfico.
x
|
y
|
(x,Y)
|
-4
|
7
|
(-4,7)
|
-3
|
0
|
(-3,0)
|
-2
|
-5
|
(-2, -5)
|
0
|
-9
|
(0, -9)
|
2
|
-5
|
(2,-5)
|
3
|
0
|
(3, 0)
|
4
|
7
|
(4,7)
|
Veja que o gráfico
corta o eixo das abscissas nos pontos -3 e 3, enquanto que o ponto mínimo da
parábola tangencia o eixo de y em -9.
2-
Construir o gráfico da função: y= x2 + 4x – 5
O gráfico
corta o eixo das abscissas nos pontos -5 e 1, enquanto que o ponto mínimo da
parábola tangencia o eixo de y em -9.
Quando
a parábola tem a concavidade voltada para cima dizemos que a função possui um
MÍNIMO.
3- Construir, no plano cartesiano, o
gráfico da função y =-x2 - 4
Atribuindo alguns valores para x,
encontramos o valor de y. Depois traçar o gráfico e marcar os pontos.
y =-x2 - 4
Y = -(4)2 – 4 = -16 – 4 =
-20
Y = -(3)2 – 4 = -9 – 4 = -13
Y = -(2)2 – 4 =- 4 – 4 =
-8
Y
= -(0)2 – 4 = 0 – 4 = -4
x
|
y
|
(x,Y)
|
-4
|
-20
|
(-4, -20)
|
-3
|
-13
|
(-3, -13)
|
-2
|
-8
|
(-2, -8)
|
0
|
-4
|
(0, -4)
|
4-
Construir o gráfico da função: y= - x2 + 4x – 5
O gráfico
tem como vértices (2, -1)
O gráfico
não corta o eixo das abscissas no ponto, isto é, não tem raízes nos reais.
Quando
a parábola tem a concavidade voltada para baixo dizemos que a função possui um
MÁXIMO.
1º Determinar as coordenadas do Vértice: V(Xv,
Yv).
2º Organizar uma tabela, onde se atribuir alguns
valores menores que Xv e
alguns valores maiores que Xv .
3º Marcar os pontos no plano cartesiano no eixo das x
(abscissas) e eixo das y( ordenadas).
4º para finalizar é só ligar os pontos construindo a
parábola.
O VÉRTICE
DA PARÁBOLA: As
coordenadas do vértice da parábola são dadas por:
Exemplos:
1) Achar o máximo ou o mínimo da função f(x)=x2 – 2x
– 8
A função tem o mínimo igual a -9.
Outra maneira para encontrar o vértice de y, substituir o valor encontrado de x na
função. Veja como fica:
f(x)=x2 – 2x – 8
y= 12 – 2 .1 – 8
y= 1 – 2 – 8 = -9
Vejamos o gráfico dessa função:
A função tem o mínimo igual a -9.
Outra maneira para encontrar o vértice de y, substituir o valor encontrado de x na
função. Veja como fica:
f(x)=x2 – 2x – 8
y= 12 – 2 .1 – 8
y= 1 – 2 – 8 = -9
2) Achar o máximo ou o mínimo da função f(x)= - x2
+ 6x – 9
A função tem o máximo igual a 3.
Outra maneira para encontrar o vértice de y, substituir o valor encontrado de x na
função. Veja como fica:
f(x)=-x2 – 6x – 9
y= 32 – 6 .(-3) – 9
y= - 9 +18 – 9 = 0
3)
Achar o máximo ou o mínimo da função f(x)= - x2 - 2x +1
A função tem o máximo
igual a 2.
4) Achar o máximo ou o mínimo da função f(x)= x2 + 3x - 4
Em uma outra postagem estudaremos OS SINAL DA FUNÇÃO.















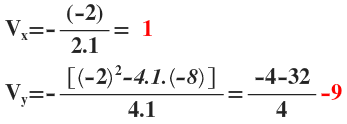





calcule a raiz de cada função, em seguida construa o grafico a) f(x)=2x-3 b) f(x)=-x+2 c)f(x)=-3x-4 d)f(x)=x-1
ResponderExcluirgrafico da função quadratica , resolucao de a=-x² b=-2x c=+3 tabela????
Excluirno blog tem uma pasta por de "dicas" lá tem um aplicativo que faz o gráfico. Neste espaço não tenho como ajudar.
ExcluirVocê também pode atribuir valor pra x e encontrar o valor de y.
y=-x^2 -2x + 3 exemplo
y= -0^2 - 2.0 + 3
y = 3
Enquanto: x=0 y=3
Você pode atribuir quantos números quiser
y= -x^2 -2x + 3
y= -(-1)^2 - 2. (-1) + 3
y= -1 + 2 + 3
y= 4
enquanto x = -1 y=4
depois você marca no plano cartesiano e traça a parábola.
Obrigado foi muito útil
ResponderExcluiry=x-6+5
ResponderExcluirComo acho a, b c se y=(x-3).(x+2)
ResponderExcluirSinal para indicar x ao quadrado " ^ "
Excluir1° resolve os produtos dentro dos parênteses
y= x^2 + 2x - 3x - 6 simplificando ou reduzindo
y= x^2 - x - 6 observe que temos uma função do 2° grau (x^2 - x - 6 = 0)
a= 1
b= -1
c= -6
Gente por favor me ajudem não sei fazer esses construção de gráficos a) x²-4x+4
ResponderExcluirb) -x²+4x+4 c) x²-4 d) x²+3x
O certo é você seguir os passos ensinados na postagem para construir seus gráficos.
ExcluirNo início do meu blog tem uma pasta como o nome "DICAS" lá você vai encontrar um aplicativo que vai lhe dar o desenho do gráfico.
Maneira de escreve sua função para que o aplicativo possa dar a resposta correta.
Sinal usado para dizer que um número é elevado ao quadrado "^"
Escreva assim:
y = x^2 - 4x + 4
Ele vai dar o gráfico dessa função.
y=x^2 + 4x + 4
E assim por diante.
A letra B escrevi errado esta faltado o sinal de menos
Excluira) y=x^2 - 4x + 4
b) y=-x^2 +4 + 4
c) y=x^2-4
d) y=x^2 +3x
Basta escreve cada função no aplicativo como foi explicado acima.
Sem fazer o gráfico, determine as cordenadas do vértice (xv yv) dos pontos em que a parabola corta o eixo x: a) -2x ao quadrado +12x. Alguém mim ajude pra hj pra agora.
ResponderExcluirSem fazer o gráfico, determine as cordenadas do vértice (xv yv) dos pontos em que a parabola corta o eixo x: a) -2x ao quadrado +12x. Alguém mim ajude pra hj pra agora.
ResponderExcluirSua função pelo que entendi é y = -2x^2 + 12x ou f(x) = -2x^2 + 2x é a mesma coisa simbolo usado para dizer que -2x elevado ao quadrado (^)
ExcluirAntes vou dividi os valores de a e b por 2. Ficando assim: y = -2x^2 + 12x
O vértice de x divide a parábola ao meio, nesse caso as raízes vai ser ( 0, 6)
Para encontrar o vértice de x é só dividi o valor de b por 2a ( b/2a ). Em seu caso 6/2 que vai ser 3.
Para encontrar o vértice de y é só dividi -delta por 4a. Em seu caso 36/4 que vai dar 9
Vx = 3
Vy = 9
Dada a função y==x²-2x-4, esboce a parábola achando as raízes, o xv e o yv???
ResponderExcluirGabrielly, aqui nos comentários não tem como tirar suas dúvidas.
ExcluirPara encontrar as raízes é só você resolver a equação do 2° grau. x²-2x-4=0
Que são os valores (raízes de x), onde a parábola corta o eixo de x.
O vértice de Vx é a parte onde a parábola é divido ao meio, isto é, o meio da parábola.
O vértice de Vy é a parte onde mostra a curvatura toca o eixo de y.
No meu blog tem uma pasta com o nome "DICAS" lá tem um aplicativo que pode ajudar.
Digite: x^2-2x-4=0.
Padre me ajuda. Frazer essa
ResponderExcluirF(x)=4X-4 depois está assim determine o zero (valor de x quando f(x)=0)da função
F(x)=4x-4 essa é uma função do 1° grau.
Excluir4x-4=0 divide os dois membros por 4 para encontrar o valor de x ou seja, o zero da função. Que é a raiz que ao ser substitiuda no x anula a função.
4x-4=0
x=4/4 ( sinal para indicar divisão /)
x=1 (raiz ou zero da função)
A questão ainda pede o seguinte f(x)=0
É só substitui na função o x por 0 r resolver.
f(0)= 4x-4
f(0)= 4. 0 - 4
f(0) = 0 - 4
f(0) = - 4
QUANDO E DADA A FUNÇÃO F(X)= X2 + 6X - 12
ResponderExcluirVocê não diz o que quer, se o gráfico da função ou o zero da função, ( zero da função são as raízes da função)
ExcluirPara calcular o zero das função é só igualar a função a zero e depois resolver como se resolver uma equação do 2° grau.
x^2 + 6x - 12 =0 (^ sinal para indicar que x foi elevado ao um número)
No meu blog tem uma pasta com o nome de DICAS lá tem um aplicativo que pode te ajudar.
Digite assim
x^2 + 6x - 12 = 0
Boa sorte
Como represento em um mesmo sistema cartesiano a função, y = X² ?
ResponderExcluirComo represento em um mesmo sistema cartesiano a função, y = X² ?
ResponderExcluirÉ só atribuir alguns valores para x que você vai encontrar o valor de y. Lembrando que se trata de uma função do 2º grau.
ExcluirExemplo:
quando x=0 ---- y será( y=0 )
quando x=2 ------ y=4
x= -2 ----------- y= 4
Construa no plano cartesiano o gráfico da função f (x)=-x^2+6x-5 por favor me ajude
ResponderExcluirConstrua no plano cartesiano o gráfico da função f (x)=-x^2+6x-5 por favor me ajude
ResponderExcluirConstrua no plano cartesiano o gráfico da função f (x)=-x^2+6x-5 por favor me ajude
ResponderExcluirConstrua no plano cartesiano o gráfico da função f (x)=-x^2+6x-5 por favor me ajude
ResponderExcluirNo blog tem uma pasta com o nome de DICAS lá tem um aplicativo que vai dar o gráfico.
ExcluirDigite -x^2+6x-5=0
Para entende função do 2° grau, antes devemos estudar equações do 2° grau. Uma coisa esta relacionada com a outra.
Oque eu faço quando eh assim 2 (x²-2x+6) ?????
ResponderExcluirAjudem-me pfvrrrrrr
Pelo que você escreveu trata-se de uma equação do 2º grau completa. O número 2 que esta fora dos parenteses, é multiplicado por cada um dos valores que estão dentro. Depois é só resolver.
Excluir2x² - 4x + 12
Neste blog tem o assunto e na pasta por nome DICAS tem um aplicativo que vai dar os valores das raízes.
Para digitar no aplicativo, digite assim: 2x^2-4x +12=0
Com relação a sua questão você ainda deve lembrar que se menor que zero, no conjuntos dos números reais não tem raiz. Delta nesse caso deu -80. Sendo assim não tem raiz.
ExcluirObservação: Se você faz o ensino médio e já estudou ou esta estudando o conjunto dos números complexos, você deve ter aprendido que nesse caso os números negativos tem raiz.
Ao usar o aplicativo você vai encontrar x'= 1-i raiz quadrada de 5 x''=1+i raiz quadrada de 5
F(x)=x^-4x-5=1/2
ResponderExcluirF(x)=x^-4x-5=1/2
ResponderExcluirBoa noite Maria! Não consegui entender a sua expressão matemática. Veja no youtube digite o nome do assunto e veja lá alguns vídeos, para que possa tirar suas dúvidas. Boa sorte.
ExcluirComo resolver essa função y=(x-3)²
ResponderExcluirConstrua o gráfico da função quadratica
ResponderExcluirA) y=3x²-3x+1
B) y=x²+8x
Bom dia Carina! O espaço aqui não dar para construir gráfico. No meu blog tem um aplicativo que vai te ajudar ele fica na pasta de DICAS.
ExcluirA letra (A) delta é menor que zero. logo a parábola não corta o eixo de x.
Você pode atribuir valores para x e encontrar o valor de y. Depois é só marcar no plano cartesiano esses pontos e traçar sua parábola. Veja o exemplo.
y=3x²-3x+1
y=3.1²-3.1+1
quando x for 1 y=1
y=3x²-3x+1
y=3.2²-3.2+1
y=7
quando x for 2 y=7 ( assim por diante, depois é só traçar os pontos marcado no plano cartesiano)
B) y=x²+8x essa tem raízes, isto é, o eixo de x vai ser cortando em zero ( 0) e em (-8)
Você pode fazer o mesmo processo que foi feito para encontrar outros pontos, depois é só marcar no plano cartesiano e traçar seu gráfico.
ALGUÉM ME AJUDA , NÃO SEI NEM COMO COMEÇAR A FAZER UM GRÁFICO
ExcluirConstrua no plano cartesiano o gráfico da função f (x)=x^2+x-6 Por favor me ajude
ResponderExcluirConstrua no plano cartesiano o gráfico da função f (x)=x^2+x-6 Por favor me ajude
ResponderExcluirConstrua no plano cartesiano o gráfico da função f (x)=x^2+x-6 Por favor me ajude
ResponderExcluirProfessor me ajude por favor.é pra hoje essa questão.
ResponderExcluirProfessor me ajude por favor.é pra hoje essa questão.
ResponderExcluirMe ajude nesta questão pfvr..a) Y=x^2-2x
ResponderExcluirZelia Ramos, você não disse qual é o problema. Se o zero da função (raízes) ou gráfico.
ExcluirPara o zero da função você deve antes transformar a função em uma equação,que nesse caso é uma equação do 2°grau, isto é, no lugar de y coloco um zero.
Y=x^2-2x
x^2-2x = 0 (equação do 2° grau incompleta. Tenho a=1 e b= -2)
Colocando x em evidencia, efetuando a divisão.
x^2-2x = 0
x(x-2) = 0 igualando x=0 esse é uma raiz
x-2 igualando
x-2=0 jogando -2 para o segundo membro, lembrando de mudar o sinal.
x=2 essa é a segunda raiz.
Boa sorte.
Y=-2x^2+4x+6 me ajude x',x",xv,yv
ResponderExcluirY=-2x^2+4x+6 me ajude x',x",xv,yv
ExcluirPara encontrar as raízes ou zero da função, você deve igualar a função a zero, transformando em uma equação do 2° grau. Depois é só resolver.
-2x^2+4x+6=0
x'=-1
x''=3 são as raízes da equação.
Para encontrar o vértice de x e o vértices de y no blog tem uma explicação passo a passo.
Vx= 1
Vy=8
Boa sorte
Determine as raízes reais se houver, e esboce os gráficos das seguintes funçoes : y = x² - 3
ResponderExcluirDetermine as raízes reais se houver, e esboce os gráficos das seguintes funçoes : y = x² - 3
ResponderExcluiry= 3 x^{2} +2 \sqrt{3} x+1 como faz para resolver essa questao quando tem raiz
ResponderExcluirPelo que entendi tratar-se de uma função do 2° grau.
ExcluirPara encontrar a raiz de qualquer função seja ela do 1º ou do 2º grau, você antes tem que igualar a zero.
Depois resolve do seguindo os passos aprendido antes quando estudou equações do 1º grau ou 2° grau.
O que é igualar a zero?
É simples basta você tirar o y e no lugar colocar zero. Você vai ver que ficou uma equação, em seu caso uma equação do 2° grau.
Do jeito que você escreveu sua função não ficou muito claro não.
f (x)=ax^+bx+x.sabendo que f (1)=4, f (2)=0 e f (3)= -2
ResponderExcluirNão entendi a questão. Se você aprendeu equação do 2º grau na 8ª série você vai consegui resolver função, seja ela do 1º grau ou do 2º grau. É só igualar a função a zero e calcular as raízes depois construir o gráfico.
ExcluirQuando o professor dar uma função e logo em seguida colocar algo como f(2)=..... Ele esta pedido que você substitua na função dada o X pelo valor dado no parenteses, depois é só efetuar as operações indicadas na função.
ExcluirMe ajuda!!! Quando tenho uma função quadrática que é assim:
ResponderExcluiry=-2x^2+72
Preciso do zero da função, e o gráfico...
tem outra que é assim:
y=-x^2+4x
Novamente, preciso do zero da função eo gráfico... por favor, eu não entendi isso .-.
Carlos Você para encontra o zero da função é fácil. Você tira o y ( ou f(x) )
Excluire iguala a zero. Resolve do mesmo jeito que você aprendeu em equação do 2º grau.
O zero da função na verdade é as raízes dessa função, isto é, o número que substituindo na função original vai zerar a função.
Quanto ao gráfico aqui não dar para fazer.
y=-2x^2+72
2x^2 - 72 =0 ( você pode dividi ambos membros por 2 ficando assim.
x^2 - 36 = 0 ( coloque 36 dentro do radical para tirar a raiz) nesse espaço não é possível desenha o radical. Outro desenho que não é possível depois do x coloque o sinal de mais e menos
x = Mais ou menos raiz quadrada de 36. Extraindo a raiz.
x= 6
x= -6
O gráfico vai contra nesses dois pontos. E a boca da parábola vai esta voltada para baixo.
y=-x^2+4x
-x^2 + 4x =0
x^2 - 4x = 0 ( insolando o x e dividindo ao mesmo tempo)
x( x - 4) = 0
x = 0 primeira raiz.
(x - 4)
x-4 = 0
x = 4 segunda raiz
o gráfico vai passa por esse pontos.
No meu blog tem uma PASTA com o nome DICAS, nela você pode digita cada uma das funções, do mesmo jeito que você escreveu aqui, que ele vai dar o desenho do gráfico de cada uma das funções.
Eu quero um gráfico é uma tabela dessa função f(x)=3-2
ResponderExcluirf(x)=3-2 eu não entendi. Aqui neste espaço dos comentários é impossível traça qualquer gráfico.
ExcluirNo meu blog tem uma pasta de DICAS, lá tem um aplicativo que vai fazer isso para você.
Agora tem que escreve a função correta.
Do jeito que você fez ele não vai aceita.
Se for do primeiro grau você deve digitar
Exemplo:
3x-2=0
Se for do segundo grau
Lembre que no aplicativo tem uma explicação de como digitar.
Por exemplo:
um número elevado a outro.
3^2
Multiplicação
3*2
construa o grafico da função y=x ao quadrado-2x-3 quanndo indentificando os coeficientes a b e c?
ResponderExcluirDada a função y=x²-5x+6 construa uma tabela atribuindo valores inteiros entre -2 e 5 para a variavel x e construa o seu grafico
ResponderExcluirO professor deu a função e disse para você atribuir valores entre -2 e 5 e depois construir o gráfico.
ExcluirExemplo: No lugar onde tive x você substitui pelos valores,para encontrar o valor de y
y=x²-5x+6
y=(-1)²-5(-1)+6
Y=1+5+6= 12
y=x²-5x+6
y=(0)²-5(0)+6 =6
y=(1)²-5(1)+6 =2
y=(2)²-5(2)+6 =0
y=(3)²-5(3)+6 =0
Você vai marcar no plano cartesiano esses pontos.
Observe que 2 e 3 (raízes) são por onde o eixo da parábola vai corta o eixo de x.
Os pontos de y=( 0, 2, 6, 12, ...)
Os pontos de x=(-1, 0, 1, 2, 3, 4,...)
com relaçao á funçao f(x) = - x² + 3x + 4, determine as raizes ( caso existam), o maior ou menor valor e esbolce o grafico.
ResponderExcluirVocê iguala a função a zero, e resolve seguindo os passos que você aprendeu em equação do 2ºgrau. Para encontrar as raízes.
ExcluirNeste espaço não para construir o gráfico. No blog na pasta de Dicas existe um aplicativo que faz o gráfico.
As raízes são (-1, 4)
No eixo das abscissas o gráfico vai passar por -1 e 4
alguém sabe me responder isso com gráfico =-x2 + 4X-4
ResponderExcluirNa postagem se você segui os passos dado vai responde qualquer questão que o professor passar.
ExcluirNo blog também tem uma pasta com o nome DICAS lá tem um aplicativo que pode ajudar.
basta digita a função assim:
-x^2 + 4x - 4=0
Boa sorte
Alguém sabe me responder isso com gráfico y=x2+5x+2
ResponderExcluirNeste espaço não tem como construir um gráfico.
ExcluirNa postagem se você segui os passos dado vai responde qualquer questão que o professor passar.
No blog também tem uma pasta com o nome DICAS lá tem um aplicativo que pode ajudar.
basta digita a função assim:
x^2 + 5x + 2=0
Boa sorte
Como eu Fasso quando e y=x^-x-6 mim ajudar prfvvv
ResponderExcluirVocê colocou: y= x^-x - 6
ExcluirNão dar pra saber do que se trata.
Se você quis dizer que x é elevado a dois, tudo bem. Tratar-se de uma função do 2º grau.
Outra coisa, você não disse o que o professor quer, se é o gráfico dessa função ou o zero da função.
Se a função for essa:
y=x^2 - x - 6 você iguala a zero
x^2 -x - 6 = 0 e resolve como se fosse uma equação do 2º grau para encontrar as raízes ( zero da função)
No blog tem uma pasta com o nome de dicas , se você digitar essa função como escrevi ele vai desenhar pra você o gráfico
alguem pode me ajudar, todos são x elevado a 2
ResponderExcluirx2-x-20=0
x2-3*-4=0
x2-8x+7=0
Luis Henrique, pelo jeito se trata de equações do 2º grau. No blog tem várias postagens como conteúdo e até mesmo exercícios respondidos passo a passo.
ExcluirInfelizmente aqui neste espaço não dar para resolver.
Você pode usar a fórmula de Bhaskara para resolve-lá
Luis der uma olhada em seu Email.
Como faço esse grafico da função do segundo grau y=x²-2x e y=x²+3x
ExcluirNo resumo acima dei vários exemplos de como construir o gráfico da função.
ExcluirUma das maneiras é você encontrar as raízes e ela existirem.
Sabendo que as raízes corta o eixo das abscissas. E depois traça o gráfico, observando também os vértices de x e de y
Na primeira função a parábola tem a vértice y -2
Aqui neste espaço não tem como desenhar o gráfico.
Qualquer coisa, no meu blog na pasta de DICAS tem um link que vai levar você por outro site chamado DESMOS, lá você pode digitar sua função e vai aparecer o gráfico construído.
O bom é você fazer sozinho para treinar e aprender e na dúvida você vai no site para conferir se acerto.
Bons estudos.
Determine os zeros ou as raízes de cada funções quadráticas
ResponderExcluira)y=x2-6x'6
b)y=2x2-3x+
Do jeito que você digitou não dar para entender.
Excluira)x elevado ao quadrado -6x (depois você digitou 6. Não sei o que você quis dizer)
b) 2x elevado ao quadrado -3x ( depois você digitou + não sei o que você quis dizer)
Determinar as raízes (zeros) reais da função de R em R dada pela seguinte lei: y=(x+3).(x-5)
ResponderExcluirVocê vai resolver a multiplicação.
Excluiry=(x+3).(x-5)
y=x^2 -5x +3x - 15 ( ^ sinal para dizer que x foi elevado ao quadrado). Agora é só igualar a zero e resolver a equação do 2° grau.
y=x^2 -5x +3x - 15
x^2 -5x +3x - 15 = 0
x^2 -2x - 15 = 0
Solução
x' = 5
x'' = -3
O grafico representa no cartesiano da função f(x)=x elevado ao cubo+ax+bx+3.a soma de a+b é igual a?
ResponderExcluir"Encontre As Raízes e Faça o Espaço Do Gráfico Das Funções
ResponderExcluirF(x) = 4x2 - 2x"
"Encontre As Raízes e Faça o Espaço Do Gráfico Das Funções
ResponderExcluirF(x) = 4x2 - 2x"
Para encontrar as raízes você iguala a função a zero: 4x^2 - 2x = 0
ExcluirE resolve como você aprendeu na equação do 2º grau.
Lembrando para construir o gráfico você tem que ver se a equação tem raízes.
Se tiver uma raiz o gráfico só topa o eixo de x.
Se tiver duas raízes o gráfico corta o eixo de x em dois pontos.
Se não tiver raiz não encontra no eixo de x.
Você que ver se a boca vai esta voltada para cima ou para baixo.
O seu exemplo a boca vai esta voltada para cima. Tem duas raízes.
(0, 1/2) são aos raízes zero e um meio.
Neste espaço não dar para traçar o gráfico.
Me ajudem porfavor a pergunta e essa
ResponderExcluirEsboce o gráfico da função quadrática.y=x -13x+42
No blog tem esse assunto. Função do 1° grau.
ExcluirEste espaço não dar para fazer o gráfico.
Na pasta "DICAS" tem um link do site DESMOS que faz o gráfico.
O gráfico nesse caso é uma reta.
Determine os zeros das funções quadraticas e faça o esboço do gráfico.
ResponderExcluirA) Y=-x²+2x+3
B) Y= x²-2x+1
C) Y= x²-2x-1
Isso vale 5 pontos
Se conseguir respoder eu agradeço muito.
Obrigado muito bom
ResponderExcluir