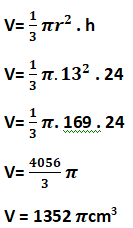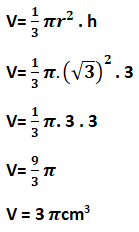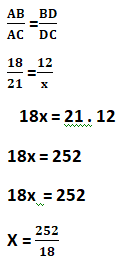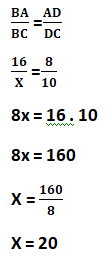15 de dez. de 2022
5 de dez. de 2022
VOLUME DO CONE
Resumo do volume do cone
O volume de um cone é obtido da mesma maneira que o volume da pirâmide.
O volume de uma pirâmide é o terço do produto da área da base pela medida da altura
Exemplos:
1) Qual o volume do cone sabendo que o raio da base é 3 cm e a altura 4 cm?
Substituindo os valores na fórmula:
2) Ache o volume de um cone com diâmetro 26cm e 24 cm de altura.
Raio mede 13 cm
3) Sabendo que o raio a base de um cone equilátero mede raiz quadrada de 3 e que sua altura é 3 cm, qual o volume desse cone?
26 de nov. de 2022
VOLUME DO CILINDRO
Só lembrando que para calcular o volume de um prisma, basta multiplicar a área da base pela medida da altura. Veja o exemplo abaixo. Qual é o volume de água que cabe no aquário ao lado, que tem orma de um paralelepípedo e dimensões 84 cm, 60 cm e 36 cm?
V= ( 84 . 60) . 36
V = (5.040) . 36
V= 181.440
Lembrando que:
181.440 cm3
1 cm3
= 1 ml
Logo o volume que cabe nesse prisma é de 181.440 ml
Como calcular o volume do cilindro
Vcilindro = Abase . altura
Calculando o volume do cilindro abaixo
V = 3,14 .
32 . 8
V = 3,14 . 9 . 8
V = 226,08
cm3
Qual o volume do cilindro cujo raio mede 3 cm e a altura 2 cm
V = 3,14 . 32 . 2
V = 3,14 . 9 . 2
V = 56,52 cm3
12 de out. de 2022
NÍVEL DE INSTRUÇÃO EDUCACIONAL DOS MORADORES DO POVOADO BOM JESUS
Escola Municipal Leonídio Leite
Professor orientador: Vergniaud
Quanto ao Nível de Instrução educacional dos moradores do Povoado Bom Jesus.
Alunos (as): Any Carolainy, Deisy Cláudia, Gessiano, Kawanne e Maria Eduarda
A pesquisa foi realizada pelos alunos (as) através de perguntas aos moradores do Povoado Bom Jesus/ Laranjeiras-SE. faixa de idade dos entrevistados eram de 15 a 75 anos. Segue abaixo os dados.
Legenda:
F.I – Ensino Fundamental Incompleto
F.C – Ensino Fundamental Completo
M.I – Ensino Médio Incompleto
M.C – Ensino Médio Completo
S. I – Ensino Superior Incompleto
S.C – Ensino Superior Completo
C.T – Curso Técnico
30 de set. de 2022
SISTEMA DE 1° GRAU: MÉTODO DA SUBSTITUIÇÃO
Resolver os sistemas usando o método da SUBSTITUIÇÃO:
3ª - GINCANA DE MATEMÁTICA - 2022
ESCOLA MUNICIPAL LEONÍDIO
LEITE
Professor organizador:
Vergniaud dos Santos Sé, com apoio dos professores (as), equipe diretiva e
equipe de apoio.
Objetivo: Estimular a curiosidade, interesse,
participação e criatividade do discente, para que o mesmo explore novos
caminhos na aplicação da Matemática, contribuindo e facilitando na aprendizagem
da mesma. Desenvolvendo um trabalho em equipe, responsabilidade e cooperação
entre os envolvidos.
As atividades a serem desenvolvidas se darão em dois
momentos:
1- Aulas extras, no
turno contrário para o desenvolvimento das atividades: 2, 5, 11.
2- Apresentação e o desenrolar das atividades com todos os presentes, onde serão avaliados.
REGRAS E TAREFAS
1) Os alunos terão de tolerância 15 minutos na chegada, depois disso o portão será fechado não permitindo a entrada e saída de nenhum aluno.
2) Há um tempo limite para cada questão, terminado o tempo, caso algum grupo não tenha terminado, deverá entregar a atividade mesmo assim.
3) A atividade que estiver totalmente correta recebe a pontuação máxima.
4) Caso a questão esteja incorreta ou incompleta, será considerado a parte realizada e lhe atribuído o devido valor.
5) A classificação se dará pela soma de pontos de cada equipe.
6) Quando o grupo terminar a atividade antes do tempo determinado deverá levantar a mão e aguardar até que seja recolhida a atividade.
7) A atividade de n° 6 a equipe que não soube a resposta pode passar a pergunta para a outra equipe, se essa não soube poderá repassar a pergunta. A equipe responde ou paga, com isso não perdera ponto. A equipe que à risca responde e erra perdera 10 pontos por cada resposta errada.
8) A equipe que faltar com respeito à equipe adversária será punido com perda de pontos (tipos: vaias, brigas, xingamentos ...).
9) Os representantes que durante a realização das tarefas receberem ajuda dos colegas a equipe será desclassificada. Perdendo pontos para a equipe adversária.
10) Havendo empate, o critério de desempate se dará pela maior pontuação a partir da primeira rodada de questões até que não haja mais empate.
11) Quaisquer outras observações não presentes, serão observadas posteriormente e em comum acordo com a maioria dos participantes.
12) O Grupo
que ficar em 1º lugar receberá ........... pontos para
ser adicionado com a IV avaliação na disciplina de Matemática.
13) O grupo
que ficar em 2º lugar, receberão ............ pontos
para ser adicionado com a IV avaliação na disciplina de Matemática.
ATIVIDADES A SEREM DESENVOLVIDAS PELAS EQUIPES
1- Grito de guerra:
A equipe deverá elaborar um grito de guerra. A avaliação dessa tarefa levara em consideração:
-Coerência na letra;
-Animação da equipe;
-Criatividade;
-Envolvimento de toda equipe.
50 pontos
2- Tangram: Apresentação de montagem de figuras
com as peças do tangram: 4 pessoas por equipe. Número máximo de figuras: 2
figuras por equipe.50 pontos.
3- Tangram: Tarefa surpresa feita na hora usando
as peças do tangram: 2 pessoas por equipe.50
pontos.
4 – Caça- palavras com temas relacionados a assuntos de Matemática– 2 pessoas por equipe. Marca ponto quem encontrar todas as palavras primeiro.
Tempo máximo: 10 minutos. 50 pontos
5- Malha Geométrica- Apresentação
de desenhos geométricos feitos pelos alunos. 4 pessoas por equipe. Número máximo de
2 cartolinas por equipe. 100 pontos.
6- Perguntas e resposta. Perguntas surpresas. 6 pessoas por equipe.
Observação: A equipe que não soube a resposta pode passar para a outra equipe, se não soube pode devolver para a primeira equipe. A equipe pode responder ou pagar.
A equipe que responder errado perde 10 pontos por cada resposta errada.
Tempo:5 minutos. 10 pontos
7- Paródia ou rap. Cada equipe, de no máximo 10 pessoas, deverá parodiar uma música a critério, com temas relacionados à matemática. Tempo máximo: 10 minutos. 50 pontos
8- Circuito maluco. Vence a equipe que chegar primeiro no ponto final. 2 pessoas por equipe.
50 pontos
9- Desafios surpresa cálculos matemáticos: 5 pessoas por equipe.
Cada equipe irá resolver o desafio: Marca pontos a equipe que resolver em menor espaço de tempo.
Tempo máximo: 15 minutos. 100 pontos
10-Quebra cabeça: 2 pessoas por equipe:
Tempo máximo10 minutos. 50 pontos
11 – Desenhos:
Apresentação de desenhos feitos em cartolinas, usando o conceito de
proporcionalidade. 4 pessoas por equipe. Máximo de desenhos 2 por equipe. 100 pontos.
12 – Construção de figuras geométricas tridimensional com dobraduras: 6 pessoas por equipe. 100 pontos.
Observação: As tarefas serão feitas por alunos diferentes, isto é, todos da equipe devem participar.
|
3ª GINCANA DE MATEMÁTICA 2022 ESCOLA MUNICIPAL LEONÍDIO LEITE DATA:........../........./2022 HORÁRIO: ............... h/min. Local: Escola Municipal Leonídio Leite |
13 de ago. de 2022
EXERCÍCIOS COM TEOREMA DE TALES NOS TRIÂNGULOS
Toda reta paralela a um lado de um triângulo determina, sobre os outros dois lados, segmentos proporcionais.
1) Determine o valor de x, sabendo que DE // BC
3) Observe o mapa as ruas Colibri, Pardal e canário são paralelas. Determine as distâncias de x e y.
6) Calcule o valor de x.
27 de jul. de 2022
CALCULANDO A METADE DE UM NÚMERO NA FORMA DE POTENCIAÇÃO
1) A metade do número 213 é igual a:
a) 26.5 b) 212 c) 221 d) 113 e) 112
2) (FUVEST-SP) Qual a metade de 222 ?
Respostas:
1) A metade do número 213 é igual a:
Vamos dividir a potência 213 por dois, ficando assim:
Podemos escrever essa divisão assim
213 : 2
Aplicamos uma das regras de
potenciação que diz: Divisão de potências de mesma base, repete-se a base e
subtrai os expoentes.
213 : 2 = 213-1
= 212
Resposta correta letra B.
2) (FUVEST-SP) Qual a metade de 222 ?
Para responder essa segunda questão, segue os mesmos passos da primeira.
221
13 de jul. de 2022
24 de jun. de 2022
23 de mai. de 2022
PROBLEMAS ENVOLVENDO EQUAÇÃO DO 2° GRAU
1) Um terreno retangular tem 1100 m2 de área. A frente desse terreno tem 28 metros a menos que a lateral. Quais são as dimensões desse terreno?
2) O piso de um galpão retangular tem 140 metros quadrados de área. As medidas dos lados desse piso, em metros, estão indicadas na figura. Quais são essas medidas?
3) Um terreno retangular de 80 m por 50 m, foi construído um barracão que serve de depósito para uma firma. Esse depósito ocupa uma área de 1000 m2 . Em torno do barracão, há um recuo de x metros de cada lado para um gramado (ver figura). Qual é a medida x desse recuo?
Respostas:
1) Um terreno retangular tem 1100 m2 de área. A frente desse terreno tem 28 metros a menos que a lateral. Quais são as dimensões desse terreno?
Vamos representar o lado desse terreno por x.
x = lado
(x - 28 )= frente do terreno
1100 m2 =terreno
Montando a equação
x ( x - 28) = 1100
x2 - 28x = 1100
Resolvendo a equação do 2° grau para encontrar o valor de x.
Resposta: 50 m e 22 m
2) O piso de um galpão retangular tem 140 metros quadrados de área. As medidas dos lados desse piso, em metros, estão indicadas na figura. Quais são essas medidas?
3) Um terreno retangular de 80 m por 50 m, foi construído um barracão que serve de depósito para uma firma. Esse depósito ocupa uma área de 1000 m2 . Em torno do barracão, há um recuo de x metros de cada lado para um gramado (ver figura). Qual é a medida x desse recuo?
80 e 50 Lados do terreno
x é o recuo
1000 m2 área total do terreno.
(80 - 2x ) ( 50 - 2x) = 1000
4000 - 160x - 100x + 4x2 = 1000
4x2 - 260x + 4000 - 1000= 0
4x2 - 260x + 3000 = 0 dividindo tudo por 4.
x2 - 65x + 750 = 0
Resposta final.
x < 50 m
x = 15 m