O dispositivo permite encontrar o quociente e o resto da divisão de um polinômio P(x) de grau n (n> 1) por um binômio x-a, sendo (n -1) o grau do quociente.
Vejamos um exemplo prático de como fazer:
a) Efetuar a divisão (x3 +2x2 – x + 3) : (x - 1)
1º passo:
Devemos determinar a raiz do binômio x - 1
x = 1, nesse caso a raiz é 1.
colocamos a raiz encontrada nesse caso 1 no lado esquerdo. como mostra o esquema abaixo, enquanto os coeficientes no lado direito:
2º passo:
Abaixe o primeiro coeficiente e multiplique pela raiz e depois some com o segundo coeficiente, coloque o resultado abaixo, isto é ao lado do primeiro coeficiente. E assim o processo será repetido até o último coeficiente.
1 . 1 = 1 multiplica 1 pela raiz, resultado soma com o 2.
1 +2 = 3 colocar-se o 3 no quociente.
3 . 1 = 3 multiplica 3 pela raiz, resultado soma com o -1.
3 + (-1)= 2 colocar-se o 2 no quociente.
2 . 1 =2 multiplica 2 pela raiz, resultado soma com o 3.
2 + 3 = 5 este número é o resto da divisão.
3º passo:Organizando tudo:
Os três primeiros números são os coeficientes. O último número é o resto da divisão.
Lembrando que o quociente terá sempre um grau a menos do dividendo:
Quociente: Q(x)= x2 + 3x + 2
Resto: R(x) = 5
b) Efetuar a divisão (4x3 - 2x2 +3x -1) : (x +2)
calculando a raiz ( x + 2)
x = -2 (raiz do binômio x + 2 é - 2)
Efetuando a divisão
4 . (-2)=-8
-8 + (-2) = -10
___________________
-10 . (-2) = 20
20 + 3 = 23
___________________
23 . (-2) = -46
-46 + (-1) = - 47 é o resto da divisão
Organizando:
Q(x)= 4x2 - 10x + 23
R(x)= -47
c) Efetuar a divisão (x4 + 2x3 + x - 6) : ( x - 3)
Observe que o polinômio é do 4º grau, incompleto. Para isso precisamos arrumar, ficando assim:
x4 + 2x3 + 0x2 + x + 46
calculando a raiz de ( x - 3)
x = 3
Efetuando a divisão:
1 . 3 = 3
3 + 2 = 5
_____________
5 . 3 = 15
15 + 0 = 15
______________
15 . 3 = 45
45 + 1 = 46
______________
46 . 3 = 138
138 + (- 6) = 132 o resto da divisão
Q(x)= x3 + 5x2 + 15x + 46
R(x)= 132
Agora é com vocês:
Utilizando o dispositivo de Briot-Ruffini, determine o quociente Q(x) e o resto R(x), da divisão dos polinômios abaixo:
a) (x2 - 7x + 12) : ( x - 5 )
b) (2x3 - 4x2 + x - 3) : ( x - 1 )
c) (4x3 - 3x + 4) : ( x - 4 )
RESPOSTAS:
a)
Q(x) = x -2
R(x) = 2
b)
Q(x) = 2x2 - 2x -1
R(x) = - 4
c)
Q(x)= 4x2 + 16x + 61






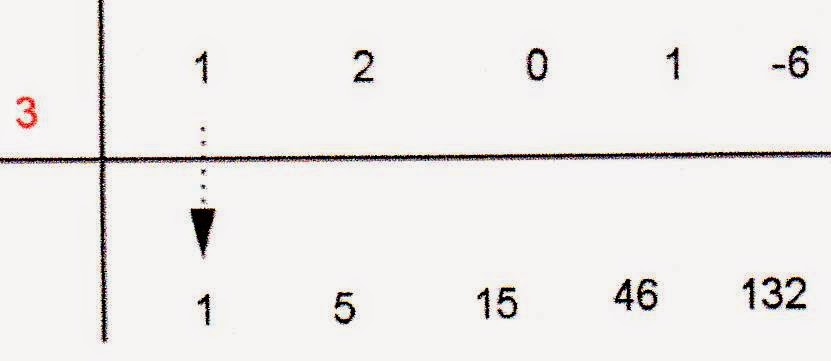
Respostas para b y c son incorrectas
ResponderExcluirPara verificar se as respostas estão corretas basta multiplicar o quociente pelo divisor e adicionar o resto se tiver.
ExcluirRealmente a resposta "B" está incorreta
Excluir47 e não -47
ExcluirEsta certo. Você multiplica 23 por -2 = -46
ExcluirDepois você soma com -1
(-46) + (-1) = -47
Só seria 47 positivo se fosse uma multiplicação.
Na adição, soma-se e conserva-se o sinal.
Tá errada essa parada aí fera.
ResponderExcluirO que esta errado?
ExcluirEu acho que o resto do exercício b esta errado....
ResponderExcluirmuito bom amei ...
ResponderExcluirusando un dispositivo pratico de briot ruffini obtenha o quoeficiente Q(x)e R(x)da divisao de P(x) =x3+5x-1porx-2e
ResponderExcluirVocê observe a cima passa a passo os exercícios. Aqui não tem com montar e responde.
ExcluirA resposta final é.
Q (x) = x^2 + 2x + 9 ( ^sinal para dizer que x é elevado a 2)
R(x) = 17
Boa sorte.