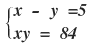1) Resolver os sistemas abaixo:


2) A soma das áreas de dois quadrados é 52
cm2 Sabendo que a diferença entre as medidas dos lados desses quadrados é 2 cm, calcule a área de cada quadrado.
3) A diferença entre as idades de Pedro e Joana é 5 anos, e o seu produto é 84. Qual a idade de cada um?
4) A soma de dois números é 28, e diferença entre o quadrado do primeiro e o quadrado do segundo, nessa ordem, é 56.
5) Determine dois números inteiros e positivos tais que o produto entre eles seja 140, e a diferença entre eles seja 4.
RESOLUÇÃO:
Vamos usar o método da substituição. Qualquer dúvida vá até a postagem
SISTEMA DE EQUAÇÃO DO 2º GRAU, lá tem um resumo passo a passo de como se resolve um sistema do 2º grau.
1)

Como x é igual a 2y, é só substitui na segunda equação.
x=
2y
x + y2 = 35
2y + y2 = 35 organizando temos uma equação do 2° grau
y2 + 2y – 35 = 0
a= 1; b= 2 ; c= -35
Encontrando o valor de x.
x= 2
y
x= 2.
5
x=10
x=2
y
x=2 .(
-7)
x= -14
Solução: (10,5); (-14, -7)
 x = 9 - y
x = 9 - y ( substituindo x na 2ª equação)
xy = 14
(
9-y).y =14
9y – y2 = 14
– y2 + 9 – 14 = 0 (multiplicando por -1 ).
y2 - 9 + 14 = 0
Encontrando o valor de x.
x = 9 -
y
x = 9 -
7
x = 2
x = 9 -
y
x = 9 -
2
x = 7
Solução: (2, 7); (7, 2)

x =
5 - 2y ( substituindo na 2ª equação)
y2 = 7 – 3x
y2 = 7 –
3.(5 – 2y)
y2 = 7 – 15
+ 6y ( organizando)
y2 - 6y + 8
= 0
a= 1; b = - 6; c = 8
Encontrando o valor de x.
x = 5 - 2
y
x = 5 - 2
.4
x= -3
x =
5 - 2
y
x = 5 - 2
.2
x=1
Solução: (-3, 4); ( 1, 2)

x =
-17 + 2y ( substituindo na 2ª equação)
y2 + 5x=
-29
y2 + 5( -
17 + 2y) = -29
y2 - 85 +
10y = -29
y2 + 10y - 85 + 29 = 0
y2 + 10y - 56 = 0
x = -17 + 2
y ( encontrando o valor de x. )
x = -17 + 2.
4
x = -17 + 8
x= -9
x = -17 + 2
y
x = -17 + 2 . (-14)
x = -17 - 28
x= - 45
Solução: (-9, 4); ( -45, -14)
2) A soma das áreas de dois quadrados é 52
cm2 Sabendo que a diferença entre as medidas dos lados desses quadrados é 2 cm, calcule a área de cada quadrado.
Dados:
Vamos chamar os quadrados de x e y.
 x . x = x 2 y . y = y2
Para calcular a área de um quadrado multiplicamos a base vezes altura.
Montando o sistema:
x . x = x 2 y . y = y2
Para calcular a área de um quadrado multiplicamos a base vezes altura.
Montando o sistema:
isolando x na 2ª equação e substituindo na 1ª
x = 2 + y
y2
+ y2 = 52
(2+y)2 + y2 = 52
4 + 4y + y2 + y2 = 52
2 y2
+ 4y + 4 - 52 = 0
2 y2
+ 4y - 48 = 0 Simplificando por 2
y2 + 2y - 24 = 0
Encontrando o valor de x.
x = 2 + y
x = 2 + 4
x= 6
x = 2 + y
x = 2 + ( - 6)
x = 2 - 6
x = - 4
(6, 4)
Para a questão só interessa o números positivos.
O quadrado maior tem área igual a 36 cm2
O quadrado menor tem área igual a 16 cm2
3) A diferença entre as idades de Pedro e Joana é 5 anos, e o seu produto é 84. Qual a idade de cada um?
Solução:
x a idade de Pedro
y a idade de Joana
x = 5 + y
xy = 84
(5 +y) y = 84
5y + y2 = 84
y
2 + 5y -
84= 0
x = 5 + y ( encontrando o valor de x)
x = 5 +
7
x =
12
Observação: Os números negativos não serve para esse tipo de pergunta.
Solução: Pedro têm 12 anos e Joana têm 7 anos
4) A soma de dois números é 28, e diferença entre o quadrado do primeiro e o quadrado do segundo, nessa ordem, é 56.
Montando o sistema:
x = 28 - y ( isolando x)
x2 – y2 = 56 ( substituindo na 2ª equação)
(28 - y)2 – y2 = 56
784 – 56y + y2 –y2 = 56 ( cancelando + y2 –y2)
-56y = 56 – 784
-56y = - 728
y = -728
- 56
y = 13
Encontrando o valor de x.
x = 28 -
y
x = 28 - 13
x= 15
Solução: ( 15, 13)
5) Determine dois números inteiros e positivos tais que o produto entre eles seja 140, e a diferença entre eles seja 4.
Montando o sistema:
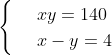
isolando x na 2ª equação e substituindo na 1ª equação
x=
4 + y
xy = 140
(
4 + y).y = 140
4y + y2 = 140
y2 + 4y – 140 = 0
x= 4 +
y
x= 4 +
10
x=
14
Solução ( 14, 10)