As Regras de três podem serem Simples ou Composta
Se o problema envolve apenas duas grandezas, será uma regra de três simples.
Se o problema envolve apenas duas grandezas, será uma regra de três simples.
Exemplo1: Um
livro tem 100 páginas, sendo que
em cada página há 40 linhas. Quantas
páginas terá este livro, se for impresso com 20 linhas por páginas?
Este exemplo envolve apenas duas grandezas: PÁGINAS e LINHAS.
A regra de três simples pode
ser: DIRETA OU INVERSA
A regra de três simples é direta, quando as duas grandezas que nela
aparecem são diretamente proporcionais, isto é, aumentando-se uma grandeza, a
outra também aumentará ou diminuindo-se uma grandeza, a outra também diminuirá.
Exemplo2: Um torneiro faz 12 peças em 3 horas. Quantas horas
gastariam para fazer 36 peças iguais às anteriores?
Uma regra de três simples é
inversa, quando as duas grandezas envolvidas forem inversamente proporcionais,
ou seja, se aumentarmos uma grandeza, a outra diminuirá e, se diminuirmos uma
grandeza, a outra aumentará.
Exemplo3: Uma casa é construída em 120 dias por 30 operários.
Em quantos dias 40 operários, com igual capacidade de trabalho, construirão a
mesma casa?
COMO RESOLVER REGRA DE TRÊS SIMPLES DIRETA
Exemplo1: Pelo
transporte de 1 300kg, paga-se um frete de R$ 286,00. Quanto se pagará pelo
transporte de R$ 1 700kg?
MASSA(kg)
|
DINHEIRO(R$)
|
1 300
|
286,00
|
1 700
|
X
|

Exemplo2:Uma máquina
produz 100 peças em 15 minutos. Quantas peças iguais às anteriores, produzirá
em uma hora?
PEÇAS(unidade)
|
TEMPO(minutos)
|
100
|
15minutos
|
X
|
1hora
|

COMO RESOLVER REGRA DE TRÊS SIMPLES INVERSA
Exemplo1: Um
serviço é feito em 5 dias, empregando-se 12 máquinas. Se fossem 10 máquinas, de
igual capacidade, quantos dias seriam gastos para executar o mesmo serviço?
MÁQUINAS (unid.)
TEMPO (dias)
12
5
10 X
Aumentando-se a
quantidade de máquinas, gastaremos menos tempo ou menos dias para realizarmos o mesmo serviço.
Diminuindo-se a
quantidade de máquinas, gastaremos mais tempo ou mais dias para realizarmos o
serviço.
ARMANDO a proporção: inverter-se a razão que não tem a incógnita.
Exemplo2: Uma
casa é construída em 120 dias por 30 operários. Em quantos dias 40 operários,
com igual capacidade de trabalho, construirão a mesma casa?
OPERÁRIOS TEMPO(dias)
30
120
40
X
REGRA DE TRÊS COMPOSTA
A regra de três composta,
envolve três ou mais grandezas e pode ser: DIRETA,
INVERSA e DIRETA E INVERSA (ao mesmo tempo).
REGRA DE TRÊS COMPOSTA DIRETA
Exemplo1: São
necessários 2 operários para fazerem, em 5 dias, 320 peças de um certo produto.
Quantas peças desse mesmo produto farão 5 operários, em 8 dias?
OPERÁRIOS
|
DIAS
|
PEÇAS
|
2
|
5
|
320
|
5
|
8
|
X
|
A
|
B
|
C
|
OPERÁRIOS
TEMPO(dias) PEÇAS
2 5 320
5 8 x
Armando:
Exemplo2: Uma loja dispõe de 20 balconistas que trabalham 8
horas por dia e recebem juntos R$ 5 000,00 por mês. Quanto a loja gastará, por
mês se tiver 30 balconista, trabalhando 5 horas por dia?
BALCONISTAS
TEMPO(dias)
DINHEIRO(R$)
20
8
5 000,00
30
5 x
REGRA DE TRÊS COMPOSTA INVERSA
Na regra de três composta inversa, apenas, uma grandeza diretamente
proporcional: aquela da incógnita X. As outras são inversamente proporcionais.
Exemplo1: Trabalhando 6 horas por dia, 10 operários fazem uma
casa em 8 dias. Quantos operários, de mesma capacidade de trabalho, serão
necessários para se fazer uma casa igual à anterior, trabalhando 2 horas por
dia, durante 12 dias?
HORAS
|
DIAS
|
OPERÁRIOS
|
6
|
8
|
10
|
2
|
12
|
X
|
A
|
B
|
C
|
HORAS
DIAS OPERÁRIOS
6 8 10
2 12 x
Comparando a primeira coluna com a coluna em que se encontra a incógnita.
horas operários
6 10
2 (-) x (+ ) (o números de operários aumentar)
dias operários
8 (-) 10
12 x (+) ( o números de operários diminui )
Observação: Os elementos das razões devem ser invertidos.
Exemplo2: Numa fábrica de calçados, trabalham 16 operários que
produzem, em 8 horas de serviço diário, 240 pares de calçados. Quantos
operários são necessários para produzir 600 pares de calçados por dia, com 10
horas de trabalho diário?
OPERÁRIOS
HORAS
CALÇADOS
16 8 240
X 10 600
Comparando a coluna da incógnita com cada uma das demais colunas.
Operários Horas
16 8 (-)
x (+) 10 (aumentando o números de horas diminui o números de operários).
Operários Calçados
16 240 (-)
x (+) 600 (aumentando o números de calçados, o números de operários aumentaras).
Nesse caso só a coluna das horas vai ser invertida.





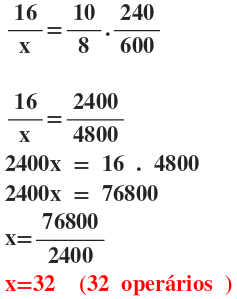
Nenhum comentário:
Postar um comentário