FUNÇÃO POLINOMIAL DE 1º GRAU

 NOÇÃO DE FUNÇÃO

As funções são  definidas abstractamente por certas relações.  Descrevem relações matemáticas especiais entre dois elementos.

As funções estão presentes em diversas situações do dia a dia, e são utilizadas também em várias ciências como na física, química, biologia, estatísticas...

Exemplos de funções polinomiais do 1ª grau:

O consumo de combustível de um carro é dado em função do percurso percorrido.

No exemplo citado, o gasto do combustível depende da distancia percorrida pelo veículo. Isto é, a variação de uma grandeza depende da outra.

Um vendedor da loja B recebe um salário fixo de (650,00?) reais mais comissão de 5% por cada venda realizada.

No final do mês seu rendimento será o seu salário mais as comissões, isto é, o salário final desse funcionário vai depende do total de vendas feitas pelo mesmo durante um mês.

Com a e b números reais quaisquer e a≠ 0, (a diferente de zero)

Toda função do tipo f(x)=ax + c ou y = ax + c,  é dita função polinomial ou função do 1º grau. Com a e b números reais quaisquer e a≠ 0, (a diferente de zero)

Exemplos:

Y= 3x -1

f(x)= 2x - 20

COEFICIENTES DA FUNÇÃO POLINOMIAL DO 1º GRAU

y=ax+b

a → é o coeficiente  angular, e a ≠ 0 

a> 0  a função é crescente.

a< 0 a função é decrescente.

b → é o coeficiente linear – é o termo independente.

Exemplo₁: f(x)= 3x – 2; onde o coeficiente de  a=3,o coeficiente de b= - 2.

a>0 logo, a função é crescente.

Exemplo₂: f(x)= -2x ; onde a=-2 e b=0, nesse caso não termos o valor de b, então b é igual a 0 (zero).

a<0 logo, a função é decrescente

GRÁFICO DA FUNÇÃO

O gráfico de uma função do 1º grau é uma reta.

Gráfico da função crescente: a>0

y= ax + b:    

F(x)= 2x – 2

vejamos como fica o gráfico dessa função que é crescente abaixo:

Gráfico da função decrescente: a<0

y= ax + b

f(x)= -2x – 2

vejamos como fica o gráfico dessa função que é decrescente abaixo:

A função polinomial do 1º grau pode ser escrita de duas maneiras diferentes que são:

y=ax+c       ou        f(x)=ax+c                

SISTEMA DE COORDENADAS CARTESIANAS      

( assunto visto no 7º ano do ensino fundamental).

Dada a função: y=x + 1. Vamos construir uma tabela atribuindo valores para x, e encontrarmos  os valores 

de y.

x	Y=x + 1	y	(x,y)
-2	Y=-2+1	-1	(-2,-1)
-1	Y=-1+1	0	(-1,0)
0	Y=0+1	1	(0,1)
1	Y=1+1	2	(1,2)
2	Y=2+1	3	(2,3)

Marcando os pontos encontrados na tabela acima, no plano cartesiano abaixa. Vejamos como ficar:

Vamos marcar no plano cartesiano os seguintes pontos: (1,2),(2,4),(-1,-2),(-2,-4).

Vejamos mais um exemplo:

Dada a função: y=x + 2. Vamos construir uma tabela atribuindo valores para x, e encontre os valores de y.

x	Y=x + 2	y	(x,y)
-2	Y=-2+2	0	(-2,0)
-1	Y=-1+2	1	(-1,1)
0	Y=0 + 2	2	(0,2)
1	Y=1 +2	3	(1,3)
2	Y=2 + 2	4	(2,4)

Como o gráfico de uma função polinomial do 1º grau é uma reta, basta definir dois pares (x,y).

E traçar a reta.

O eixo x (na horizontal) é chamado de abscissas, enquanto que o eixo y ( na vertical) é chamado de ordenadas.

GRÁFICO DA FUNÇÃO POLINOMIAL DO 1º GRAU NO PLANO CARTESIANO

Vejamos os gráficos:

 y=2x                                               y=x-1                                            y= 3x + 1     

(a=2, isto é a>O)                                     (a=1, isto é a >0)                   (a=3, isto é a>0)

a>o a reta é inclinada para a direita. Essas funções são denominadas de funções crescentes. Aumentado o valor de x, o valor de y também aumenta.

a< 0 as retas são inclinadas para a direita. Essas funções são denominadas de funções crescentes. Aumentado o valor de x, o valor de y também aumenta.

Vejamos os gráficos:

           y= - 2x                                                 y= - x-1                                            y= - 3x + 1

(a= -2, isto é a<0)                                     (a= -1, isto é a <0)                   (a=-3, isto é a<0)

a< 0 as retas são inclinadas para a esquerda. Essas funções são denominadas de funções decrescentes. Aumentado o valor de x, o valor de y diminui.

DOMÍNIO E IMAGEM DE UMA FUNÇÃO

Os valores atribuídos a variável x é chamado de domínio da função e é representado por D. Os valores encontrado de y é o conjunto imagem da função, representado por Im.

Exemplo: Qual o domínio e imagem da função: f(x)=2x +1?

Atribuindo valores para x.

Y=2x+1	x	y	(x,y)
Y=2.0+1	0	1	(0,1)
Y=2.1+1	1	3	(1,3)
Y=2.2+1	2	5	(2,5)
Y=2.3+1	3	7	(3,7)

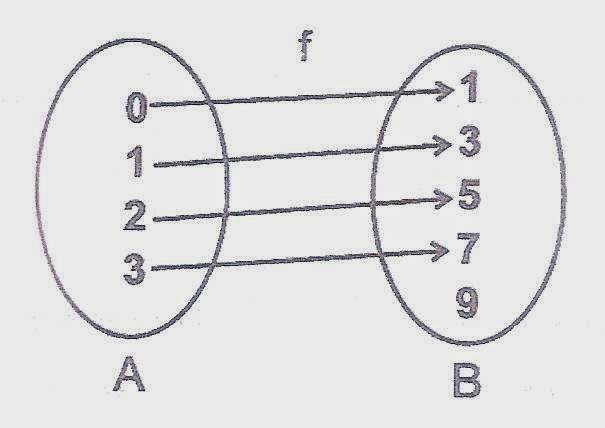
x={0,1,2,3} conjunto domínio da função

y={1,3,5,7} conjunto imagem da função

Representação através do diagrama de Venn;

O conjunto A de onde parte as fecha é o Conjunto Domínio, e o conjunto B que recebe, é o Conjunto Imagem da função dada.

ZERO DA FUNÇÃO POLINOMIAL DO 1º GRAU

Raiz ou zero da função é o valor de x pelo qual se anular a função.

Exemplo: qual a solução (raiz) da função: y=x – 3?

Igualar-se a função à zero, transformando em uma equação do 1º grau.

y = x – 3

0 = x – 3

x – 3 = 0

x= 3

x = 3

Ao substituir o 3 na função anula-se a função. Vejamos:

 y = x – 3

y = 3 – 3

y = 0

RESUMO

Uma função y=ax+b é uma função crescente quando a>0

Gráfico (a > 0)

x= -b  

      a

Uma função y=ax+b é uma função decrescente quando a<0.

Gráfico (a < 0)

x=-b   

     a

Quando a for nulo (a=0), é chamado de função constante. É representado por uma reta horizontal.

Exemplo: y=ox+2

Quando b > 0.

Exemplo: y=ox - 2

Quando b < 0.