EQUAÇÃO REDUZIDA DA CIRCUNFERÊNCIA

Vamos considerar uma circunferência 𝛽, de raio (r) e centro (C) num plano 𝛌,

 C (x_c , y_c)

x_c é o ponto das abscissas no plano cartesiano 

y_c é o ponto das ordenadas no plano cartesiano

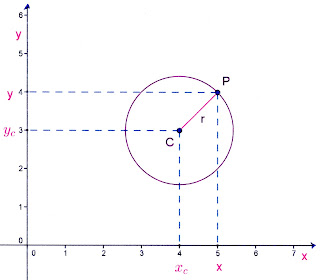
Vamos ver isso melhor no desenho abaixo.

Do ponto P (x, y) pertencer à circunferência, logo a distância do ponto P até ao centro da circunferência é igual ao raio.

d_pc = r, ou seja, o raio da circunferência é calculado pela fórmula.

(x  - x_c)² + (y – y_c)² = r²

 x_{c e} y_{c são as coordenadas do centro}

Exemplos:

a) Sabendo que o raio de uma circunferência mede r = 2 e C ( 3, -1). Qual a equação reduzida dessa circunferência?

A equação reduzida da circunferência é obtida substituindo os valores de r e C na equação reduzida. Vejamos como fica:

(x  - x_c)² + (y – y_c)² = r²

(x  - 3)² + (y – (-1))² = 2²

(x  - 3)² + (y + 1)² = 4

b) Determine a equação reduzida da circunferência cujo raio mede r =3 e C (1, 2):

(x  - x_c)² + (y – y_c)² = r²

(x  - 1)² + (y – 2)² = 3²

(x  - 1)² + (y - 2)² = 9

c) Determine a equação reduzida da circunferência cujo raio mede r =2 e C (0, 0):

(x  - x_c)² + (y – y_c)² = r²

(x  - 0)² + (y – 0)² = 2²

x² + y² = 4