É uma equação do 2º grau quando se
apresenta sob a forma: ax2 + bx + c
=0, em que a,
b e c são números reais e a≠0.
As equações do 2º grau pode ser completa ou
incompleta.
Quando b≠0
ou c≠0, a equação do 2º é completa.
Quando b=0
ou c=0, a equação do 2º grau é incompleta.
x é a incógnita.
a e b os coeficientes.
c o termo independente.
Exemplos: 3x2 – 5x + 1 =0 ⇒equação do 2º grau completa.
Termos: a=3;
b= - 5; c= 1
7x2 + 14x = 0 ⇒equação do 2º grau incompleta.
Termos: a=7;
b= 14; c= 0
9x2 – 4 =0 ⇒equação do 2º grau incompleta.
Termos: a=9;
b= 0; c= -4
RESOLVENDO EQUAÇÃO DO 2º GRAU INCOMPLETA: (
Equação do 2º grau do tipo: ax2 + c = 0
1º
transpondo a constante para o segundo membro:
ax2 + c = 0 ⇒ ax2 = -c
2º dividindo
ambos os membros da equação pelo coeficiente a.
Observação:
A equação tem duas raízes iguais (simétricas).
A equação não terá solução no conjunto dos números reais.
Exemplos:
S= {+8, -8}
Equação do 2º grau do tipo: ax2 + bx = 0
ax2 + bx = 0
Coloca-se x em evidência
x(ax + b) = 0 iguala- se x a zero
x = 0 ( 1ª raiz)
ax + b
ax = -b
Exemplos:
a)
x2 – 12x = 0
x(x – 12) = 0
x
= 0
x – 12
x
= 12
S={
0, 12}
RESOLVENDO EQUAÇÃO DO
2º GRAU COMPLETA:
Equação do 2º grau da forma: ax2 + bx + c = 0
Há vários processos de resolução de equação do 2º grau
completa, como o de Al-Khowarizmi, entre outros. Vamos usar aqui o processo
Algébico de Bhaskara por se mais fácil e pode ser usando para resolver qualquer
equação do 2º grau, seja ela completa ou incompleta.
Usando a fórmula resolutiva:
Exemplos:
a) Resolver
a equação: x2 – 7x + 6 = 0
termos: a=1;
b= -7 e c= 6
Substituindo pela as letras na fórmula.
b) Resolver a equação: x2
– x - 12 = 0
termos: a=1; b= -1 e c= -12
CONSIDERAÇÕES
IMPORTANTES
1º caso:
2º caso:
3º caso:
RELAÇÕES
ENTRE OS COEFICIENTES E AS RAÍZES


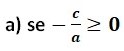










Qual e a raiz de 4x°2-3×=0
ResponderExcluirx'=0
ResponderExcluirx'' = 3/4