1) (D1)(SPAECE).
No mapa abaixo, encontram-se representadas as ruas do bairro onde Mariana
mora.
Mariana
informou que mora numa rua entre as avenidas A e B e entre as ruas do hospital
e da locadora. Mariana mora na:
(A)
Rua 4.
(B) Rua 5.
(C) Rua 7.
(D) Rua 9.
2) (D2)(SAEPE). Observe o sólido apresentado abaixo.
Uma
planificação da superfície desse sólido está representada em. (Resp. D)
3)(D16)(PAEBES). Observe
abaixo a reta numérica em que os segmentos marcados estão igualmente espaçados.
Nessa reta, os pontos que representam os
números – 2 e 3 são,
respectivamente,
A) P e Q.
B) Q e S.
C) R e S.
D) R e P.
4)(D2) (SPAECE). A figura abaixo representa um cubo em que as faces opostas
têm o mesmo símbolo.
A
planificação correta desse cubo é: (Resp. C)
5)(D1)(SPAECE). A figura abaixo representa o mapa de um bairro, em que cada
quadrado representa um quarteirão, cuja distância entre duas esquinas é de
100m.
Uma pessoa
saiu da esquina indicada pelo ponto P e percorreu o seguinte percurso:
• caminhou 300 metros na direção
Sul;
• depois
caminhou 200 metros
na direção Leste;
• e, finalmente, caminhou mais 100 metros na direção
Sul.
Ao final
desse percurso, essa pessoa chegou na esquina indicada pela letra
A)
Q
B) R
C) S
D) T
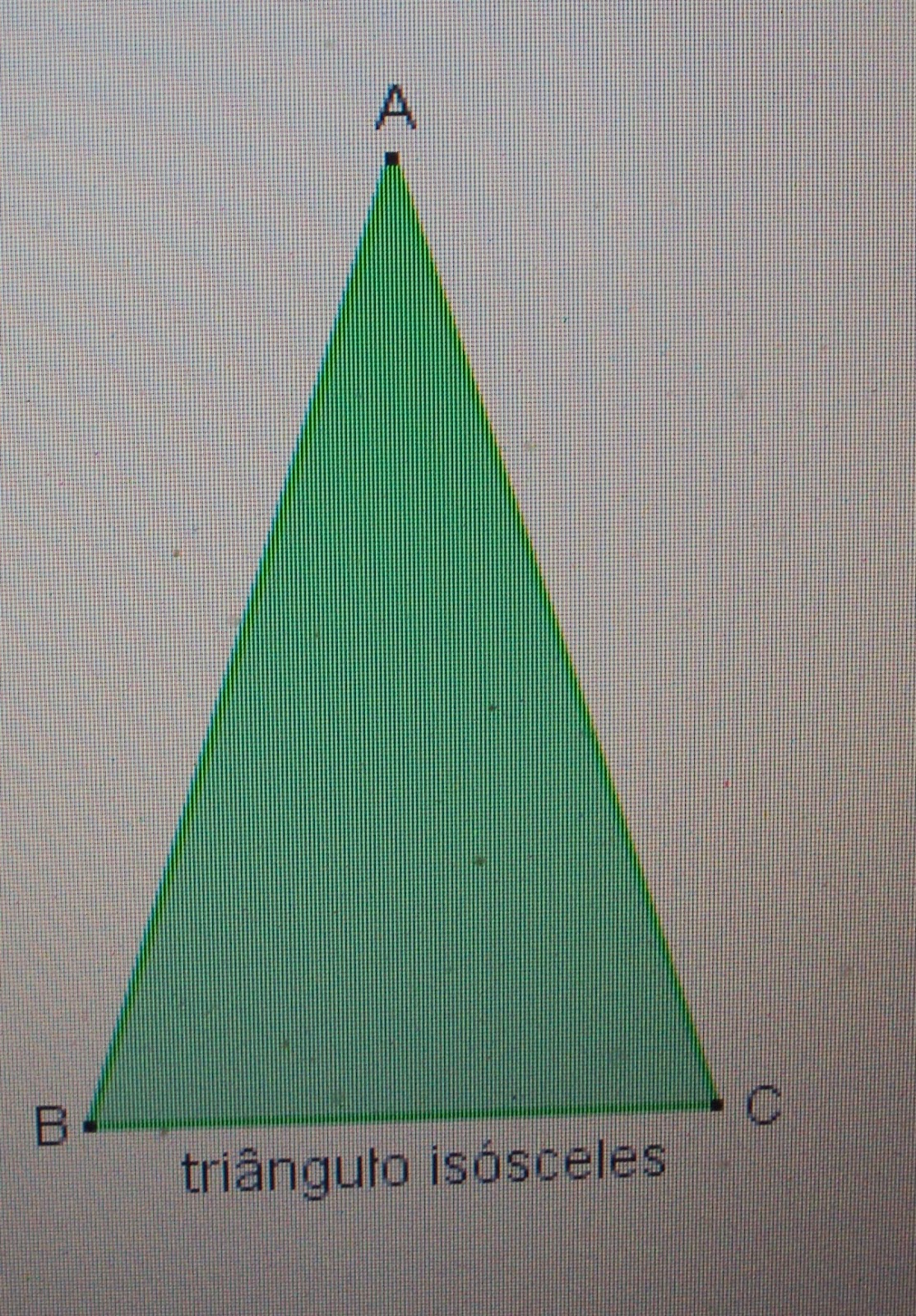
6)(D3)(SAEP 2013). Observe as
figuras.
Quanto aos lados das figuras acima
podemos afirmar que os triângulos são respectivamente
(A) escaleno, equilátero,
isósceles.
(B) retângulo, equilátero, isósceles.
(C) acutângulo, equilátero, obtusângulo.
(D) isósceles, escaleno, equilátero.
O gráfico que mostra a distribuição dos
pontos é...8)(D37)(SISPAE).
No mês de setembro, a Loja Popular vendeu 100 calças, 50
blusas, 25 pares de sapatos, 65 cintos e 80 pares de meias.
Qual é o gráfico que melhor
representa as vendas da Loja Popular nesse mês?
9)(D36)(SADEAM – AM). Para confeccionar 1
000 mL de refrigerante no sabor laranja, a Indústria Refrigerante Colorido
utiliza as quantidades de ingredientes como mostra o gráfico abaixo.
Para
fabricar 3 000 mL de refrigerante sabor laranja, as quantidades, em mL,
utilizadas de suco natural, água e corante são, respectivamente,
A)
1 350, 1 050 e 600.
B) 900, 700
e 400.
C) 600, 1
050 e 1 350.
D) 400, 700
e 900.
10)(D34)(Lousada). “A
Isabel comprou 2 kg de bananas e 3 kg de maçãs e fez uma despesa de 7 reais. Se
ela tivesse comprado 1 kg de banana e 4 kg de maçãs tinha gastado menos 1 real.
Quanto custou cada quilo de bananas e cada quilo de maçãs?” Sendo x – o preço
de cada kg de bananas e y – o preço de cada kg de maçãs. Qual dos seguintes
sistemas traduz o problema?
11)(D32)(SAEPI). A
sequência numérica abaixo pode ser definida por uma expressão algébrica, que
relaciona o valor do termo com a sua posição na sequência.
A expressão algébrica que permite
determinar on-ésimo termo dessa sequência é
A) n + 1
B) n + 2
C)
n2 + 11
D) n2
+ 34
12)(D33)(SAEP 2012).
Frederico é estudante de direito em uma Universidade pública, ele recebe uma
mesada de seu pai para suas despesas com transporte e alimentação, num total de
R$ 540,00 mensal.
Desse total ele gasta R$ 120,00 com
transporte e R$ 230,00 com alimentação.
A expressão que representa a sua economia
mensal é
(A) x –
350 = 540.
(B) x – 190= 540.
(C) x + 190= 540.
(D) x + 350= 540.
13)(D33) (Saresp –
SP). Uma locadora de bicicleta cobra R$ 20,00 por dia pelo aluguel de uma
bicicleta. Além disso, ela também cobra, apenas no primeiro dia, uma taxa de R$
30,00.
Chamando de
x o número de dias que a bicicleta permanece alugada e de y o valor total do
aluguem, é correto afirmar que:
A) y = 50x
B) y = 600x
C) y = 30x + 20
D) y = 20x + 30
14)(D30) (Camaçari). O valor
da expressão numérica abaixo é
4 + 8 x 4 + 8 – 4
÷2
A) 26
B) 54
C) 48
D) 42
15)(D28) (SPAECE). Antônio pretendia vender 500 bombons durante a feira
cultural de uma escola. Ele só conseguiu vender 50% desses bombons.
Quantos bombons ele vendeu?
A) 10
B) 250
C) 450
D) 550
16)(D21) (Prova Brasil). Observe as figuras:
Pedrinho e José fizeram uma aposta
para ver quem comia mais pedaços de pizza. Pediram duas pizzas de igual
tamanho.
Pedrinho dividiu a sua em oito pedaços
iguais e comeu seis: José dividiu a sua em doze pedaços iguais e comeu nove.
Então,
(A) Pedrinho e José comeram
a mesma quantidade de pizza.
(B) José comeu o dobro do que Pedrinho
comeu.
(C) Pedrinho comeu o triplo do que
José comeu.
(D) José comeu a metade do que
Pedrinho comeu.
17)(D19)(Prova Brasil). O
administrador de um campo de futebol precisa comprar grama verde e amarela para
cobrir o campo com faixas verdes e amarelas iguais em áreas e quantidades. O
campo é um retângulo com 100 m
de comprimento e 50 m
de largura e, para cada 10 m²
de grama plantada, gasta-se 1 m² a mais por causa da perda. Quantos m2
de grama verde o administrador deverá comprar para cobrir todo o campo?
(A) 2 250
(B) 2 500
(C) 2750
(D) 5 000
18)(D10)(PAEBES).
Um serralheiro confeccionou um portão no formato retangular com medidas de
comprimento e altura indicadas no desenho abaixo. Para uma melhor sustentação
desse portão, uma viga de aço foi colocada na diagonal desse portão.
Qual é a medida do comprimento x
da viga desse portão?
A) 5 m
B) 5 m
C)
7 m
D) 9 m
19)(D10)O senhor Geraldo
tem um compromisso às 3 horas.
Portanto,
às 3 horas, a relação entre o ângulo central (menor ângulo) e o arco
correspondente é:
(A) ângulo central é 90º e o arco 180º.
(B) ângulo central é 90º e o
arco 90º.
(C) ângulo central é 90º e o arco 180º.
(D) ângulo central é 270º e o arco 270º.
20)(18) (PAEBES). Observe a
expressão no quadro abaixo.
Qual é o resultado dessa expressão?
A) – 6,3
B) – 0,3
C) 0,3
D) 6,3
21)(D28)(SPAECE).
Alda entrou em uma loja de informática e viu o cartaz abaixo.
Alda
aproveitou essa promoção e comprou um computador cujo preço marcado em sua
etiqueta era
2 680 reais. Quanto Alda pagou por esse computador?
A)
1 340 reais.
B) 2 530
reais.
C) 2 630
reais.
D) 2 730
reais.
22) (D21) (SAEPE). O número
decimal correspondente a 25% é
A) 0,025
B) 0,25
C) 2,5
D) 25
23)(D7)(SAEP
2014). Ao incidir um facho de luz sobre um anteparo na forma do retângulo ABCD,
foi projetada em uma parede uma silhueta na mesma forma, porém ampliada.
Observando a malha quadriculada, o que ocorreu após a ampliação foi
que
(A) as
medidas dos lados foram aumentadas em duas vezes.
(B) o perímetro foi
quadruplicado.
(C) a razão
de semelhança é igual a 3.
(D) a área foi
triplicada.
24)(D28)(SAEP
2013). João comprou 1 kg de açaí congelado, como de costume ele descongelou
para fazer a sua vitamina diária e logo percebeu que o açaí estava pesando
menos de 1 kg. O peso após o descongelamento foi de 900g.
A porcentagem de gelo que
havia no açaí era de:
(A)
0,5%
(B) 10%
(C) 20%
(D) 15%
25)(D21)(SAEPE). De uma turma com 20 estudantes, 9 são
meninas. (Resp. D)
A fração que representa a quantidade
de meninas em relação ao total de estudantes dessa turma é
26)(D19)(PAEBES). Uma
companhia aérea possui um programa de fidelidade segundo o qual os clientes
acumulam pontos ao dar preferência para ela em suas viagens, podendo trocá-los,
no futuro, por passagens aéreas ou descontos, de acordo com a promoção vigente.
Joaquim, que participa desse programa, deseja adquirir uma passagem aérea dessa
companhia utilizando seus pontos acumulados e foi informado de que, para isso,
precisaria ter 33 684 pontos. Ele verificou que já possui 18 945 pontos
acumulados em sua conta.
Quantos pontos Joaquim
ainda precisa acumular em sua conta para adquirir essa passagem aérea?
A) 14 739
B) 18 945
C) 25 341
D) 52 629