1) Determine
o valor de x em cada uma das figuras, sabendo que:
RESPOSTA:
7x = 168
x=168
7
x= 24
RESPOSTA:
5x – 5 = 3x
5x – 3x = 5
2x= 5
x = 5
2
x = 2,5
RESPOSTA:
x+1 = 3
4 x
x2 + x = 12
4 x
x2 + x = 12
x2 + x – 12
= 0 equação do 2º grau
RESPOSTA:
4 = 3x - 1
6 4x+2
4.( 4x + 2) = 6.( 3x – 1 )
6 4x+2
4.( 4x + 2) = 6.( 3x – 1 )
16x + 8 = 18x – 6
16x -18x = -6 – 8
-2x = - 14 (-1)
2x = 14
x = 14
2
x = 7
2) No triângulo ABC da figura abaixo temos que DE//BC Sabendo que a medida do lado BC do triângulo é 14 cm, calcule as medidas dos lados AB e AC o perímetro desse triângulo.
RESPOSTA:
x -1 = x + 4
3 x
x.( x -1 ) = 3.( x + 4 )
x2 – x = 3x
+ 12
x2 – x - 3x
– 12 = 0
AB = 8 cm, AC = 16 cm
Perímetro: 8 + 16 + 14
= 38 cm
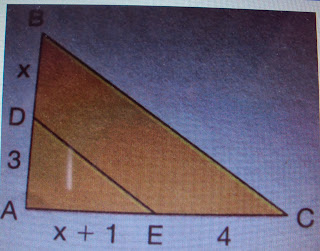
3) No triângulo da figura abaixo, as medidas são consideradas em
centímetros. Se BC=32 cm, calcule o valor de x – y.
RESPOSTA:
x = 10
y 6
como, BC = x + y = 32, podemos aplicar um das propriedades da proporção.
x + y = 10 + 6
y 6
32 = 16
y 6
16y = 192
y = 192
16
y=12 cm
Sendo y = 12 cm; x= 20 cm
Resposta final: x – y = 20 – 12 = 8 cm
4)Uma quadra de um loteamento tem a forma da figura abaixo. Na
figura estão indicadas,em metros, algumas medidas dessa quadra. Como DE é paralelo a BC,
a quadra foi dividida em dois lotes. Determine o perímetro de cada um desses
lotes.
RESPOSTA:
160y = 7200
y = 7200
160
y= 45
Se y= 45, logo x= 120 – 45 = 75
x = 75 e y = 45
Calculando
os perímetros dos lotes.
Lote 1
100 + 75 + 30 = 205
metros
Lote 2
60 + 45 + 30 + 50 = 185
metros.
5) Considere um triângulo ABC, onde o lado AB mede 18 cm, e o lado BC mede 12 cm.
Traçamos uma reta paralela ao lado BC do triângulo, que irá cortar o lado AC no ponto D e o lado BC no ponto E, tal forma que AE = 9cm e EC = 3
cm.
Descubra as medidas dos segmentos AD e BD .
RESPOSTA:
Em primeiro lugar vamos
fazer o desenho do triângulo ABC.
x = 9
y 3
x + y = 9 + 3
y 3
18 = 12
y 3
12y = 54
y = 54
12
y= 4,5 cm
x = 18 – y
x = 18 – 4,5
x = 13,5
cm
6) Duas avenidas têm
origem em um mesmo ponto A e cortam duas ruas paralelas, como mostra a figura:
Na primeira avenida, os quarteirões determinados pelas ruas paralelas medem 50 m e 80 m, respectivamente. Na segunda avenida, partindo de A, a medida do primeiro quarteirão é 36 m menor que a medida do segundo quarteirão. Qual é a medida dos quarteirões dessa segunda avenida?
RESPOSTA:
50 = x -36
80 x
80x – 2880 = 50x
80x -50x = 2880
30x = 2880
x= 2880
x= 96
x – 36
96 – 36 = 60
Resposta final: um mede 60 metros e o outro 96 metros.
7) Dois postes perpendiculares ao solo estão a uma distância de 4 m um do outro, e um fio bem esticado de 5 m liga seus topos. Prolongando esse fio até prendê-lo no solo, são utilizados mais 4 m de fio. Observe a figura:
Determine a distância entre o ponto onde o fio foi preso ao solo e o poste mais próximo a ele.
RESPOSTA:
4 = x
5 4
5x = 16
x = 16
5
x= 3,2 metros
(Conquista da Matemática 8ª série: EXERCÍCIO DA
PÁGINA 210)


















nao
ResponderExcluirjhonatan<----
ResponderExcluirmeu nome é rosiele , sou muito ruim em matemática esse site mim ajudou a resolve algumas das minhas duvidas sobre teorema de tales , mas ñ pude deixa de nota que tem algumas atividades erradas como a atividade "d" pois 6x3 e igual a 18 e esta escrito como 16
ResponderExcluirObrigado, Rosiele pelo comentário, e continue estudando, pois sem o estudo não somos nada. Quanto ao erro pode acontecer principalmente na hora de digitar.
ResponderExcluirMas, você esqueceu de dizer qual é a" questão."
Se foi a "d" da 1º questão, esta correta. É que na hora de resolver usamos uma das propriedades das proporções, que diz: O produto dos extremos é igual ao produto dos meios. Ficando assim:
4 . ( 4x + 2) = 6 . ( 3x - 1)
16x + 8 = 18x - 6
Me enrolei na questão 5.
ResponderExcluirNo enunciado você fala: a reta paralela ao lado B do triângulo, que irá cortar o lado AB no ponto D e o lado BC no ponto E
Acabei de não conseguindo desenhar a figura e quando olhei o seu desenho, notei que o ponto E corta o lado AC e não o lado BC conforme seu enunciado.
Pode verificar?
Obrigado pela observação: O erro foi meu ao digitar. Faltou um pequeno detalhe. Que já foi corrigido.
Excluir" Traçamos uma reta paralela ao lado BC do triângulo."
O desenho esta certo e a resolução também. Mas, foi muito bom sua observação.
Um abraço.
tenho uma duvida quando as duas raizes da equacao do 2 grau for positiva qual sera o valor do x no teorema de tales seria a soma dos dois
ResponderExcluirNo geral o professor quando elabora uma questão dessa, geralmente uma raiz é positiva e a outra negativa. Agora se por a caso as duas venha a se positiva, você vai ter que usar um outro artificio para descobrir a resposta correta.
ExcluirVocê sabe que o triângulo tem três lados e um assunto visto na 7ª série (8º ano) é a condição de existência de um triângulo que diz:
EM QUALQUER TRIÂNGULO, A MEDIDA DE UM LADO É SEMPRE MENOR QUE A SOMA DAS MEDIDAS DOS OUTROS DOIS LADOS.
Exemplo: Um triângulo tem a seguintes medidas. 13cm; 6,9cm e 7,2cm
13cm < 6,9cm + 7,2cm = 14,10cm
Outro exemplo:
Um triângulo mede 7cm e 2 cm quanto mede o terceiro lado?
7 < 2 + x
7 - 2 < x
5 < x logo x tem que ser maior que 5
A medida do terceiro lado vai ser 6cm.
Espero ter tirado sua dúvida.
olá, não tem como imprimir os exercícios. obrigado
ResponderExcluirDrielly da Silva Mancilla, é verdade as postagens não tem como imprimir, foi por isso que criei uma pasta com o nome: DOWNLOAD. Lá você pode baixar, imprimir. Não sei se tem o que você esta procurando.
ExcluirMuito obrigado
ResponderExcluirEste comentário foi removido por um administrador do blog.
ResponderExcluirQuando juntaram na 2: -(+4) não era pa ter dado -4 ao invés de +4?
ResponderExcluirNa questão 2. o termo b da questão esta negativo (-4) com o negativo da formula fica positivo. Ao substitui na formula fica negativo.
Excluir