EXERCÍCIOS COM POTENCIAÇÃO

Usando os conhecimentos das regras de potência:

1) A metade de 2²²  é:

a) 1                       

b) 11                    

c) 2²¹                        

d) 2¹¹

2) A metade de 16²⁰  é:

a) 8¹⁰                       

b) 2⁷⁹                     

c) 16⁴                        

d) 8²⁰

3) Simplificando, obtemos:

a) 2³⁶

b) 2²⁴

c) 16⁸

d) 8⁶

Resolução:

1) A metade de 2²²  é

Significa que vamos dividir o número por 2.

Resposta: C.

 

2) A metade de 16²⁰  é:

 Vamos dividir por 2. Mas antes vamos fatorar 16 para igualar as bases.

Resposta: B

3) Simplificando, obtemos:

3 elevado ao quadrado é 9

(2⁴)⁹

Potência de uma potência é só multiplicar os expoentes.

2³⁶

^{Resposta: A}

 4) a expressão ( 3 ^-2)² é igual a:

Potência de uma potência

3 ^-4   

Para eliminar o sinal negativo do expoente escrevemos em forma de uma fração, lembrado que tanto o numerador quanto o denominador é elevado a 4. 

Resposta: B

 

DESAFIO DE MATEMÁTICA

Desafio

 

1. Quantos metros tem um quilômetro?
   1.   10.000 metros
   2.   100 metros
   3.   1.000 metros
   4.   3. 000 metros
2. Qual destes números não é primo?
   1.   2
   2.   3
   3.   5
   4.   9
3. Qual a rai quadrada de 25?
   1.   4
   2.   5
   3.   6
   4.   12,5
4. Quantos graus mede um ângulo de meia volta?
   1.   90°
   2.   100°
   3.   180°
   4.   360°
5. Quantas faces tem um cubo?
   1.   10
   2.   12
   3.   6
   4.   4
6. Quanto mede o lado de um guadadro, sabendo que sua área mede 49 metros quadrado?
   1.   4 metros
   2.   6 metros
   3.   7 metros
   4.   8 metros
7. Qual destes números é divisível por 2 e 3 ao mesmo tempo?
   1.   204
   2.   207
   3.   219
   4.   328
8. Quantas arestas tem um cubo?
   1.   6
   2.   8
   3.   10
   4.   12
9. Quando um número é divisível por 6?
   1.   Quando é divível por 3
   2.   Quando é divível por 2
   3.   Quando é divível por 2 e 3 ao mesmo tempo
   4.   Quando é par
10. Lú têm 5 blusas e 6 shorts, de quantas maneiras diferentes ela pode se vestir?
    1.   11
    2.   15
    3.   25
    4.   30

DIVISÃO COM NÚMEROS NATURAIS

 

No quociente eu posso colocar qualquer número de 0 a 9, e assim vou efetuando a divisão, veja um exemplo passo a passo.

a) Qual é o resultado da divisão de 5 6 8 4 5 por 2?

Observe que 5 é maior que ( 2 ) o divisor, sendo assim posso dividir. Tenho que encontrar um número que multiplicado pelo divisor seja igual ou menor que o 5. Nesse caso é o 2, pois  2 x 2 = 4. 

Se eu colocar 3 vai passar, 3 x 2 = 6

Pego esse 4 e subtrai do 5, sobrou 1, agora desço o próximo número e continuo a divisão.

Observe que 16 é maior que o divisor, sendo assim posso dividir. Tenho que encontrar um número que multiplicado pelo divisor seja igual ou menor que o 16. Nesse caso é o 8,  pois 8 x 2 = 16

Se eu colocar 9 vai passar, 9 x 2 = 18

Pego esse 16 e subtrai do 16, sobrou 0, agora desço o próximo número que é 8  e continuo a divisão.

E assim vai seguindo esses passos até não ter mais número para dividi

Efetue a divisão de 7 5 4 6 por 3

E quando o divisor for mais de um número? 

O processo é o mesmo. Vejamos um exemplo:

Uma granja tem 19440 ovos de codorna que devem ser acondicionados em caixas contendo 36 ovos cada uma. Quantas caixas serão necessárias para acondicionar todos os ovos?

Observe que 1 é menor que o divisor. 

19 também é menor que o divisor

194 é maior que o divisor.

Começamos a divisão por 194.

DIVISÃO COM NÚMEROS NATURAIS

A divisão é o contrário da multiplicação ( inverso). Para isso o aluno precisa dominar bem a multiplicação, antes do estudo da divisão. 

I - A divisão é usada quando queremos dividir uma quantidade em partes iguais.

Exemplo: Um professor quer dividir uma turma de 40 alunos em equipes de 5. Quantos alunos ficará em cada equipe?

Em cada equipe ficará 8 alunos.

II - Quantas vezes uma quantidade cabe em outra.

Exemplo: Para colocar 192 ovos em caixas, sabendo que cada caixa cabe 12 ovos. Quantas caixas serão necessárias?

São necessárias 6 caixas.

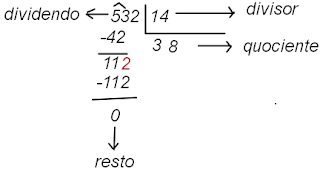
TERMOS DA DIVISÃO:

RELAÇÃO UNDAMENTAL DA DIVISÃO

Dividendo = divisor x quociente  +  resto

   396        =    15     x    26    +    6

O processo inverso é:

Quociente x Divisor + Resto = DIVIDENDO

         26   x      15        +    6     =   396  

( ao fazer isso, se o resultado não for igual ao dividendo a divisão está errada).

Como a divisão o resto foi zero, dizemos que essa divisão é exata.

 

Como nessa divisão o resto foi diferente de zero dizemos que essa divisão não é exata. 

Observações:

a) Nem todo número natural pode ser dividido por outro número natural.

      

Não existe um número que multiplicado por 0 que dê 7. Logo, por não existe divisão zero.

b) Nem sempre a divisão a divisão de dois números naturais dá um número natural.

O número 2,25 não é um número natural (2,25  IN; não pertence a IN)

c) Quando o dividendo é 0, e o divisor é um número natural diferente de 0, o quociente é 0.

Quando multiplicamos 0 por 5 dá zero.

d) Quando o dividendo e o divisor são números naturais iguais e não nulo, o quociente é 1.

e) O resto da divisão de dois números naturais sempre vai ser menor que o divisor.